Математическое ожидание и дисперсия. Мода и медиана

Определение: Средним значением или математическим ожиданием непрерывной случайной величины  называется значение интеграла

, где 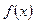 – плотность вероятности.

Предполагается, что интеграл сходится абсолютно.

Определение: Дисперсией НСВ  называется значение интеграла .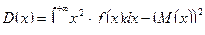

Данная формула более удобна вычисления дисперсии. Существует еще одна формула .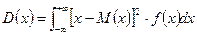

Определение: Модой 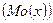 непрерывной случайной величины  называется такое значение этой величины, плотность вероятности которого максимальна или то ее возможное значение, которому соответствует локальный максимум плотности распределения.

В частности, если распределение имеет два одинаковых максимума, то его называют бимодальным.

Определение: Медианой 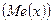 непрерывной случайной величины  называется такое её значение, при котором выполняется равенство. .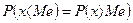

Геометрически медиану можно истолковать как точку, в которой ордината 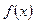 делит пополам площадь, ограниченную кривой распределения.

 

Задача 15. Случайная величина  подчинена закону распределения с плотностью 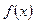, причем

 

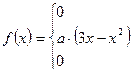
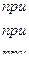
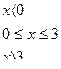
Найти

1)  коэффициент ;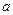

2) построить график распределения плотности ;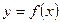

3) найти вероятность попадания  в промежуток .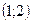

Решение:

Т.к. все значения данной случайной величины заключены на 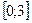, то

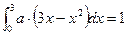откуда 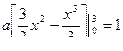, или 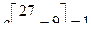, т.е. .

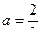Имеем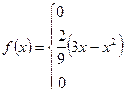    

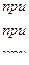
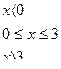
Графиком функции 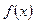 на 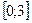 является парабола 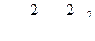, а вне этого интервала графиком служит сама ось абсцисс.

 

   

 

 

 

 

   

                                              

3

2

1

0

                                                            х

 

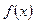
Вероятность попадания случайной величины  в промежуток 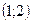 найдётся из равенства

 

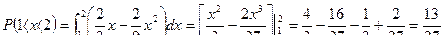
Задача 16. Случайная величина  задана плотностью вероятности:

  

 

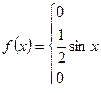
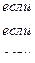
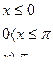
Найти , , .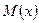

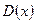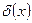Решение:

Для нахождения 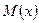 воспользуемся формулой 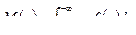. Отсюда

.

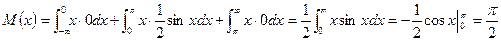Вычислим 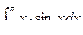 по частям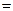

=   .

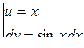
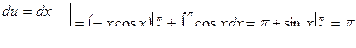Находим значение первого слагаемого в выражении дисперсии:

.

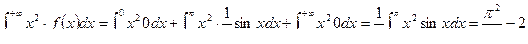
Для вычисления 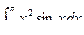 надо дважды применить формулу интегрирования по частям

 

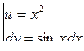
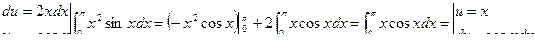
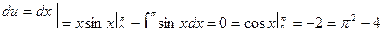
Окончательно .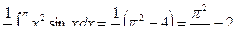

Подставляя в выражение дисперсии полученные значения, находим

; .

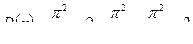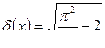Вопросы  для  самопроверки