Дифракция излучения и частиц на кристаллической решетке

Несмотря на большой прогресс в развитии техники, к настоящему времени не создано достаточно надежных и эффективных приборов, позволяющих непосредственно наблюдать расположение отдельных атомов в кристаллической решетке или в молекулах. Самые совершенные электронные микроскопы позволяют наблюдать только очень крупные атомы, например урана или золота, расположенные вблизи более мелких. Наиболее распространенные электронные микроскопы позволяют наблюдать неоднородности с размерами в несколько атомов [7]. Ионные микроскопы (проекторы) [1,8] хотя и позволяют наблюдать расположение отдельных крупных атомов, но очень сложны в использовании. Точное определение расстояний между атомами или кристаллическими плоскостями этим методом крайне затруднительно.

Сегодня самым эффективным методом изучения взаимного расположения атомов является дифракция микрочастиц: фотонов, электронов, нейтронов. Именно этими методами в основном получены данные о структуре кристаллов и молекул, помещенные в справочники. При исследовании кристалла дифракционными методами на кристалл направляют почти параллельный пучок частиц, изучают распределение интенсивности дифракции этих частиц по разным направлениям (а иногда и при различных ориентировках кристалла), а затем по дифракционной картине делают выводы о типе элементарной ячейки кристалла и строении его базиса. Эти методы позволяют определять периоды кристаллической решетки с точностью до 4-5 знака и определять с точностью до 2-3 знака расположение атомов в базисе.

Для наблюдения дифракции необходимо (см. том. 4), чтобы длина волны де-Бройля дифрагирующих частиц была меньше периодов кристаллической решетки. Этому условию удовлетворяют фотоны при энергии Е = 5-20 кэВ (рентгеновское и гамма- излучение), электроны при Е = 10-100 эВ, и нейтроны при Е = 0,01- 0,1 эВ (тепловые нейтроны с энергией порядка 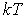). Именно эти три частицы наиболее часто используются в дифракционных исследованиях кристаллов. Наиболее просто осуществима дифракция фотонов (рентгеновское излучение, гамма излучение), поэтому их используют чаще, чем дифракцию электронов, для наблюдения которой необходим высокий вакуум, или дифракцию нейтронов, для которой в качестве источника нейтронов нужен громоздкий ядерный реактор. Дифракция нейтронов и электронов очень похожа на дифракцию фотонов, поэтому в данной главе мы подробно рассмотрим применение дифракции фотонов для изучения структуры кристаллической решетки. Эти результаты будут пригодны и для анализа дифракции нейтронов и электронов в кристалле, особенности которой будут отмечены в конце параграфа.

Кристаллическая решетка играет роль трехмерной дифракционной решетки для фотонов, электронов, нейтронов и других частиц движущихся в кристалле. Закономерности дифракции фотонов - электромагнитных волн на кристалле как трехмерной решетке можно рассчитать по той же схеме, как в томе 4 рассчитывалась дифракционная картина одномерной дифракционной решетки с N щелями, а именно, сначала рассчитывали картину от бесконечно узких щелей, а затем учитывали конечность их ширины. Получалась картина из серии наиболее ярких максимумов, интенсивность которых задавалась характером распределения интенсивности в пределах одной щели.

Рассчитаем интенсивность дифракции электромагнитного излучения (фотонов) на кристаллической решетке, имеющей примитивную элементарную ячейку в виде косоугольного параллелепипеда с векторами 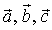. Пусть вдоль векторов 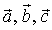решетка имеет соответственно по 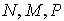узлов (см. рис. 1.13).

Рис. 1.13. Рассеяние электромагнитных волн узлами кристаллической решетки.

Пусть на такую решетку падает волна с волновым вектором 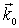, и частотой 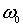, а рассеянная волна имеет волновой вектор 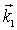Рассмотрим случай, когда не происходит изменения частоты у рассеянного излучения: , а значит (так как ) и 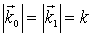. Вектор напряженности электрического поля 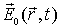в падающей волне в точке пусть задается как

 

(1.4)

В рассеянной волне вклад в вектор 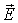от узла решетки 0, 0, 0 имеет вид:

 

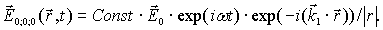
(1.5)

Волна, рассеянная на узле с номерами пройдет другое расстояние, чем волна, рассеянная на узле с номерами 0; 0; 0 (рис. 1.13). Учтем малость размеров кристалла, то есть модуля по сравнению с . Тогда . Пренебрежем также поглощением волн в кристалле. Будем считать показатель преломления для рентгеновских лучей равным 1, что выполняется с большой точностью. Оптическую разность хода между лучами, рассеянными в точках 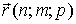и , тогда можно вычислить по формуле:

 

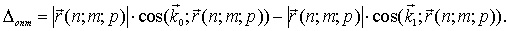
(1.6)

Разность фаз окажется равной:

 

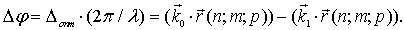
(1.7)

Вклад в вектор 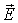от узла с номерами примет вид:

 

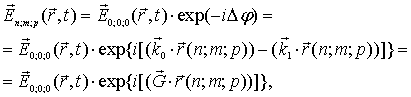
(1.8)

где 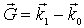- вектор рассеяния, имеющий важное значение в теории дифракции, показывающий, насколько изменился волновой вектор волны в результате рассеяния.

Вклад в амплитуду вектора 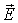от всех узлов решетки примет вид:

 

(1.9)

Суммирование в этой формуле ведется по всем узлам решетки.

Учитывая, что 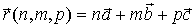, и, обозначив

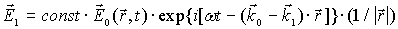, получим:

 

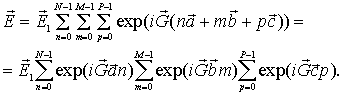
(1.10)

Выражение для представляет произведение трех сумм, первая из которых - сумма первых членов геометрической прогресси с первым членом 1 и знаменателем 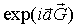. Она равна:

 

(1.11)

Аналогичные выражения можно получить и для двух других сумм. Интенсивность 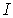равная произведению 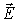на комплексно сопряженную с ней величину 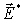после преобразований примет вид:

 

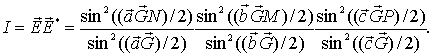
(1.12)

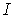максимальна и равна , если одновременно выполняются соотношения:

 

(1.13)

где 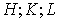- целые числа. Также интенсивность заметно отличается от нуля при условии, что величины 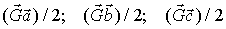отличаются от целых чисел не более чем на 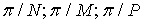соответственно.

Соотношения

 очень неудобны для анализа, между тем им можно придать очень наглядный, геометрический смысл. Для этого необходимо рассмотреть понятие обратной решетки.

Обратная решетка. Векторы основных трансляций обратной решетки определяются так:

 

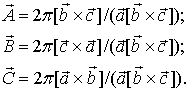
(1.14)

Можно проверить, что выполняются соотношения:

 

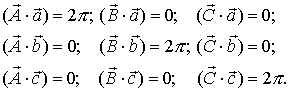
(1.15)

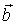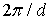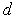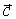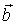Можно показать (см. задачу 1.4), что вектор перпендикулярен векторам и , а модуль вектора равен , где - межплоскостное расстояние для кристаллографических плоскостей, построенных на векторах и . Аналогичные соотношения справедливы для 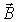и .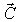

Примечание. Заметим, что определенные выше векторы обратной решетки соответствуют векторам определяемого в аналитической геометрии взаимного базиса, но их длина в 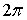раз больше. Отметим также, что векторы обратной решетки определены у нас как во многих учебниках по теории твердого тела, что обеспечивает удобство при рассмотрении движения частиц в кристалле. В учебниках по теории дифракции их определяют в точности как векторы взаимного базиса в геометрии, что позволяет исключить в во многих соотношениях теории дифракции множители .

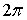Как и в случае кристаллической решетки концы векторов всевозможных трансляций 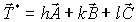, построенных на трех векторах обратной решетки, образуют также пространственную решетку, называемую обратной решеткой.

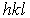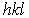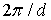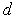Обратную решетку можно анализировать также как и кристаллическую решетку, рассматривать в ней узлы , векторы с координатами , важные направления, плоскости, координаты точек и т.д. Можно показать (см. задачу 1.5), что вектор обратной решетки с координатами , перпендикулярен плоскости кристаллической решетки с индексами Мюллера , а его длина равна , где - межплоскостное расстояние для этой системы плоскостей.

Найдем обратную решетку для кристалла с ромбической элементарной ячейкой. По формулам (1.14, 1.15), учитывая, что углы между векторами 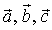- прямые, получаем:

 

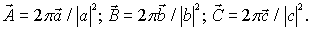
(1.16)

Видно, что самой длинной стороне ромбической ячейки будет соответствовать самая короткая сторона ячейки в обратной решетке. Аналогично можно получить, что в случае примитивной кубической решетки ячейкой обратной решетки будет куб со сторонами параллельными исходной решетке и равными .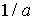

Можно показать (см. задачи 1.6, 1.7), что векторы обратной решетки в случае тетрагональной или гексагональной решетки образуют в обратном пространстве также соответственно тетрагональную или гексагональную ячейку, но с другим соотношением сторон 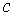и . Найти векторы обратной решетки в случае триклинной или моноклинной ячейки столь простым образом не удается, приходится вычислять их по формулам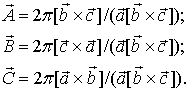

.

Вернемся к поиску векторов , удовлетворяющих условию дифракции

. Теперь им можно придать наглядный геометрический смысл. Пусть вектор разложен по :

 

.

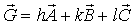(1.17)

Тогда, подставляя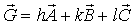

 в

 и учитывая соотношения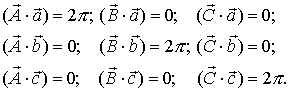

, получаем условия максимумов дифракции: 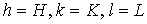, где - целые числа

Видно, что наблюдается максимум дифракции, если числа - целые, то есть, если вектор 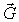совпадает с одним из векторов трансляций обратной решетки.

Можно сказать, что обратная решетка отображает дифракционную картину от трехмерной решетки. Как отмечалось в курсе оптики, дифракционная картина Фраунгофера является отображением Фурье-образа одно или двумерного распределения интенсивности излучения. Аналогично, трехмерная обратная решетка является Фурье-образом бесконечно большого кристалла, такая же решетка с узлами конечных "размеров" - Фурье-образ конечного кристалла, "размер" ее узлов (то есть областей, где интенсивность дифракции в соответствии с формулами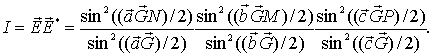

 заметно отличается от нуля) обратно пропорционален длине кристалла вдоль соответствующего направления. Вид дифракционной картины можно предсказывать, вычислив преобразование Фурье от кристаллической решетки или, как мы увидим в дальнейшем, от распределения электронной плотности в кристалле.

Обратная решетка жестко связана с кристаллической решеткой кристалла, при повороте кристалла вместе с ним поворачивается и обратная решетка. Для наблюдения дифракции кристалл поворачивают так, чтобы вектор рассеяния совпал бы с одним из узлов обратной решетки. Предсказать и наглядно изобразить это можно с помощью построения Эвальда.

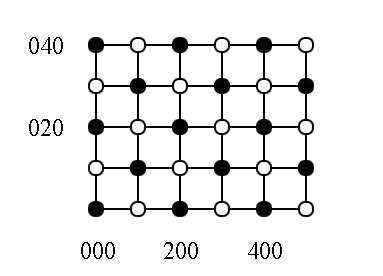
Построение Эвальда. Для предсказания углов поворота кристалла и направления дифрагированных лучей очень удобно пользоваться построением Эвальда (рис. 1.14).

Рис. 1.14. Построение Эвальда.

Отложим волновой вектор 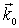падающей на кристалл волны, так что его конец совпадет с узлом 0 0 0 обратной решетки. Поскольку частота и скорость рассеянной и падающей волны совпадают, вектор рассеянной волны 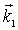будет иметь ту же длину, что и 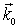, но неопределенное направление, тогда его удобно изобразить в виде сферы (сферы Эвальда) с центром в начале вектора 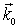. Начало и конец вектора рассеяния тогда будет соответственно концом вектора 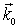и концом вектора . Теперь надо узнать, совпадет ли один из возможных векторов с одним из узлов обратной решетки. Для этого следует совместить начальный узел обратной решетки с началом вектора рассеяния (эта же точка - конец вектора 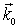) и посмотреть, попал ли один из узлов на сферу Эвальда. Ясно, что вероятность попадания одного из точечных узлов на сферу практически равна нулю, чтобы такое попадание имело место, необходимо повернуть кристалл и связанную с ним обратную решетку. Теперь уже с помощью геометрии можно вычислить необходимые углы поворота обратной решетки (и кристалла), а затем определить, под какими углами должен быть расположен детектор излучения, регистрирующий волны с вектором 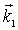. Современные приборы для наблюдения дифракции - дифрактометры, снабженные ЭВМ, позволяют в автоматическом режиме, по формулам, описывающим повороты обратной решетки, вычислять нужные углы поворота кристалла и детектора излучения для заранее сориентированного кристалла, а затем поворачивать кристалл и детектор.

На рис. 1.14 видно, что между длинами векторов 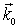и существует связь:

 

,

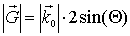(1.18)

где - известный [1,9,10] угол скольжения рентгеновских лучей. Учитывая, что 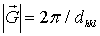(, а 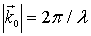получаем известное уравнение Вульфа-Брегга:

 

.

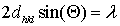В этом уравнении 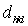содержит порядок отражения , так как , кратные одному числу, например 2; 3; 4;... учитывают порядок отражения [1].

Обратная решетка поликристалла. Поликристаллический материал, как отмечалось в разд 1.1, состоит из очень большого числа произвольно ориентированных маленьких кристаллических зерен. Каждому такому зерну будет соответствовать своя обратная решетка. Обратные решетки, отвечающие разным зернам, будут иметь одинаковые периоды и идентичное расположение узлов, но будут произвольным образом ориентированы относительно узла 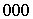обратной решетки. В таком случае узлу 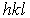обратной решетки будет соответствовать большое количество узлов (по числу кристаллических зерен), расположенных по поверхности сферы радиуса в обратном пространстве. В случае идеального поликристалла, содержащего бесконечное число случайно ориентированных зерен можно считать что узел обратной решетки превратится в сферу. Набору же всех узлов обратной решетки будет соответствовать набор таких сфер со значениями радиусов , образующих последовательность в соответствии со значениями межплоскостных расстояний кристалла. На построении Эвальда (см. рис. 1.14) в таком случае сфера Эвальда будет пересекать набор сфер по некоторым окружностям. Тогда очевидно, что дифракция от такого поликристалла окажется возможной при любой ориентации поликристалла и при любой длине волны излучения. Для наблюдения дифракции от поликристаллического образца необходимо использовать монохроматическое излучение. Подробно методики исследования поликристаллических образцов изложены в литературе по рентгеновским методам исследования [2,8,10,11].

Зоны Бриллюэна. Полезно найти множество всех волновых векторов 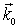волн и частиц, отвечающих условию дифракции на кристалле. Уравнение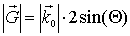

 можно переписать как:

 

.

(1.20)

Последнее есть уравнение (относительно 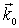) для плоскости перпендикулярной вектору и отстоящей от начала координат на расстоянии 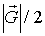. Оно же описывает возможные координаты вектора 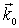, удовлетворяющие условию дифракции. Тогда множество концов векторов 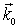, отвечающих условию дифракции, лежит на плоскостях, проходящих через середины всех векторов обратной решетки и перпендикулярных им. Именно таким способом строилась нами граница элементарной ячейки Вигнера-Зейтца в предыдущем разделе. Ячейку Вигнера-Зейтца, построенную в обратном пространстве, принято называть первой зоной Бриллюэна. Она обладает важным свойством: волны и частицы, волновой вектор которых находится на ее границе, удовлетворяют условию дифракции. Зоны Бриллюэна играют важную роль при рассмотрении движения электронов, фононов и других частиц в кристалле и при анализе энергетических зон в кристаллах (см. главы 3-5).

Структурный фактор базиса. До сих пор мы рассматривали дифракцию на кристаллической решетке, считая каждый ее узел одним точечным рассеивающим центром. С каждым таким центром обычно связаны несколько идентично расположенных атомов, называемых базисом кристаллической решетки. Волны, рассеянные на разных атомах базиса будут складываться с разными фазами в зависимости от положения атома. Схема учета вкладов в амплитуду вектора 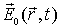дифрагированного луча такая же как и при расчете дифракционной картины трехмерного кристалла, только суммирование надо будет проводить по всем атомам базиса, а не узлам кристаллической решетки.

Пусть базис содержит несколько атомов. Обозначим за 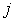номер одного из них, а через - его радиус вектор относительно начала элементарной ячейки, содержащей этот атом, а через 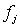- вклад этого атома в амплитуду 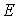вектора 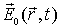рассеянной волны. Тогда вклад в амплитуду 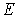для дифракции, отвечающей вектору рассеяния 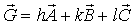, будет содержать фазовый множитель и будет пропорционален :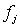

 

.

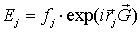(1.21)

Вклад от всех атомов базиса тогда выражается суммой по индексу :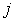

 

.

(1.22)

Учитывая, что 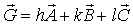и , а также соотношения

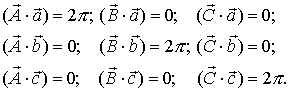
 получаем:

 

.

(1.23)

Величину 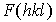принято называть структурным фактором базиса данного кристалла или же структурным фактором элементарной ячейки вещества. Эта величина будет определять относительную амплитуду дифракционных максимумов, даваемых трехмерной кристаллической решеткой. Для данного кристалла 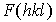зависит от вектора рассеяния, она может оказаться равной нулю для некоторого узла обратной решетки. В таком случае волны, дифрагированные разными атомами базиса, складываются, давая суммарную нулевую амплитуду, то есть погасят друг друга. При этом сама кристаллическая решетка, состоящая из "точечных узлов" могла бы обеспечить сильную дифракцию (если вектор рассеяния совпадет с одним из узлов ее обратной решетки).

Вычислим структурный фактор ОЦК решетки. Если за элементарную ячейку принять куб (см. рис. 1.1), то базис будет состоять из двух атомов с координатами 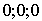и 1/2; 1/2; 1/2, и структурный фактор для узла с индексами 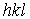обратной решетки, вычисленный по формуле

, окажется равным:

 

.

(1.24)

Видно, что 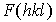равен нулю, если сумма индексов - нечетная и равен 2, если сумма индексов четная. Если теперь в обратной решетке отметить кружочками узлы с ненулевым структурным фактором, то кружочки расположатся в обратном пространстве как узлы ГЦК решетки (рис. 1.15).

Рис. 1.15. Расположение узлов обратной решетки для ОЦК решетки и структур типа CsCl

Для узлов, отмеченных светлыми кружочками на рис. 1.15, дифракции не наблюдается, так как волны, рассеянные атомами расположенными в центре кубической ячейки, будут в противофазе с волнами, рассеянными атомами расположенными в углах ячейки. Это просто объяснить с помощью рис. 1.16. На нем изображена плоскость (100) ОЦК ячейки, обозначенная как А. Видно, что параллельно ей можно провести плоскость (200), обозначенную как В, на которой будет расположено столько же атомов. Получается, что плоскости аналогичные (100) расположены как бы в два раза "гуще". Волны отраженные от плоскостей типа А при отсутствии вложенных плоскостей В усиливают друг друга, но появление плоскостей В приведет к появлению отраженной от них волны той же амплитуды, но сдвинутой по фазе на относительно волн отраженных от плоскости А. Сумма же вкладов в амплитуду дифрагированной волны от плоскостей А и В окажется равной нулю. На рентгенограммах ОЦК решетки наблюдаются отражения от плоскостей типа (110), (200), (112), (220), (130), (222) и других с четной суммой индексов. Отсутствие на рентгенограммах отражений с нечетной суммой индексов - признак ОЦК решетки.

Рис. 1.16. Отражение волн плоскостью (100) ОЦК решетки.

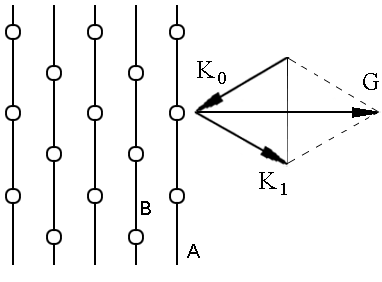
Рассмотрим теперь структуру типа цезий хлор (рис. 1.1), имеющую кубическую ячейку с базисом из двух атомов с координатами 000 - для и 1/2 1/2 1/2 - для . Ее структурный фактор, вычисляемый по формуле

, окажется равным:

 

.

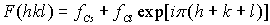(1.25)

Он не будет равен нулю ни при четной, ни при нечетной сумме индексов. В самом деле, теперь атомы расположенные в центре и по углам элементарной ячейки - разные, следовательно и рассеивают волны они по-разному 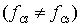. Структурный фактор окажется либо суммой, либо разностью неравных величин и 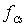. Если теперь рассмотреть, как в случае ОЦК решетки, плоскости типа А и В на рис. 1.16, то видно, что они уже разные - содержат разные атомы и будут давать разный по величине вклад в амплитуду рассеяния или одного или противоположного знака. Сумма вкладов не будет равной нулю. Поэтому узлам обратной решетки с четной суммой индексов (когда вклады атомов хлора и цезия складываются), например (200), будут соответствовать сильные дифракционные максимумы (кружочки) а нечетной сумме индексов (когда вклады атомов хлора и цезия вычитаются), например (100), - слабые дифракционные максимумы. По расположению узлов в обратной решетке тогда можно определить период решетки, а по чередованию "ярких" и "слабых" узлов - определить положение атомов в базисе решетки.

Вычислим структурный фактор ГЦК решетки. Если за элементарную ячейку принять куб (см. рис. 1.7 и раздел 1.1), то базис будет состоять из 4 атомов, и структурный фактор для узла 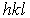обратной решетки окажется равным:

 

.

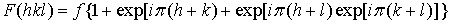(1.26)

Он равен: 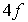, если все индексы - четные числа; 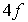, если все индексы - нечетные числа; 0, если среди индексов встречаются как четные, так и нечетные числа. Таким образом структурный фактор ГЦК решетки не равен нулю, если индексы - одинаковой четности. Можно показать (это легко сделать графически, как в предыдущей задаче), что в обратной решетке узлы с ненулевым образуют как бы ОЦК решетку. На рентгенограммах ГЦК решетки будут наблюдаться отражения от плоскостей типа (111), (200), (113), (220), (133), (222) и других с индексами одинаковой четности. Отсутствие на рентгенограммах отражений с индексами разной четности - признак ОЦК решетки.

В случае более сложных базисов структурный фактор может быть и комплексной величиной, он изменяется от узла к узлу обратной решетки по закономерностям, задаваемым расположением атомов базиса. Он определяет тем самым относительные интенсивности отражений от различных кристаллографических плоскостей. Можно решить и обратную задачу - по измеренным интенсивностям отражений определить положение атомов в базисе, то есть расшифровать структуру кристалла. Это - задача рентгеноструктурного анализа. В настоящее время расшифровано строение многих кристаллов с базисом содержащим десятки, сотни и большее число атомов.

Атомный фактор рассеяния. Пока мы не рассматривали величины, задающие амплитуду рассеяния 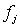от отдельных атомов, называемые атомным фактором рассеяния. Амплитуды рассеяния 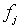могут быть либо измерены экпериментально, либо вычислены теоретически. Для такого расчета необходимо рассмотреть атом как заданное функцией распределение заряда, которое может быть мысленно разделено на маленькие элементы объема 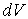. Затем следует вычислить сумму по всем этим элементам с учетом величины и разности фаз для волн, рассеянных разными малыми элементами объема (то есть по той же схеме как выше вычисляли структурный фактор базиса), но применяя интегрирование, по формуле:

 

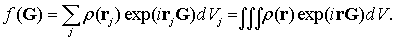
(1.27)

Величина 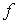в случае дифракции электронов и фотонов зависит от модуля вектора ; как правило она уменьшается при увеличении . Величина 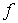больше у атомов с большими номерами, имеющих большую электронную плотность, причем спадает быстрее с ростом для атомов больших размеров, поскольку при росте разные участки атома рассеивают волны не синфазно. Атомы с близкими значениями атомного номера, то есть числа электронов, имеют как правило и близкие значения 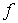. Как правило считают, что атомный фактор зависит только от - сферически симметричен. Существуют таблицы, достаточно хорошо характеризующие величины отдельных атомов в зависимости от . Отметим, что такие таблицы как правило не учитывают различия в форме внешних электронных облаков в различных кристаллах, хотя, строго говоря, форма внешних облаков и связанная с ней величина 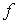зависят от окружения атома в каждом конкретном кристалле. Это с одной стороны приводит к небольшим ошибкам при вычислении 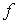, а с другой - в ряде случаев позволяет, наблюдая дифракцию, изучать перераспределение электронной плотности при образовании различных валентных связей. Величина может слегка изменяться, если энергия фотонов совпадает с одной из разностей энергий атомных уровней, из-за чего происходит также и сильное поглощение фотонов. Существуют таблицы, учитывающие и эти поправки к величине .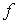

В случае дифракции нейтронов величина 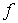складывается из ядерной и магнитной составляющих, связанных с рассеянием нейтронов на ядрах и на магнитных моментах атомов. Ядерная составляющая зависит от структуры атомного ядра и как правило оказывается различной для различных изотопов. Магнитная составляющая зависит от ориентации и величины вектора магнитного момента атома и может быть равной нулю при определенных ориентировках вектора рассеяния и магнитного момента атома. Поэтому дифракцию нейтронов используют для исследования магнитных моментов атомов в кристаллах. Подробнее об этом будет рассказано в главе 5.

Из формулы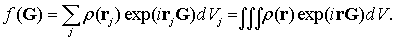

 следует, что 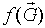представляет собой значение преобразования Фурье в точке обратной решетки задаваемой вектором от функции , задающей электронную плотность в атоме. Эту формулу можно обобщить и на базис элементарной ячейки, и на весь кристалл. Тогда вид дифракционной картины можно предсказывать, вычислив преобразование Фурье от распределения электронной плотности в кристалле. В таком случае по виду преобразования Фурье, полученному по экспериментальной дифракционной картине, можно было бы вычислять функцию и структуру кристалла, однако это сделать не удается, поскольку все известные сегодня экспериментальные методы фиксируют только интенсивность, из которой возможно определить только амплитуду Фурье-образа, а фазу зафиксировать ими не удается. Для построения функции по Фурье образу, в общем случае комплексной функции, необходима как амплитуда, так и фаза Фурье-образа. По этой причине определение структуры кристаллов решается не через вычисление функции , а прямым вычислением дифракционной картины по заданным параметрам структуры кристалла и сопоставлением вычисленной дифракционной картины с наблюдаемой. После чего таким способом проводят последовательное уточнение параметров структуры. Решением этой задачи занимается раздел физики - структурный анализ.

Упрощенные методы структурного анализа, позволяющие к примеру проводить фазовый анализ (то есть определять, из каких кристаллических решеток состоит данный материал), уже были рассмотрены в томе 5 данного курса, когда рассматривалась дифракция электронов.

Чаще всего для целей структурного анализа используют дифракцию рентгеновских лучей, поскольку ее легче осуществить с технической точки зрения. Достаточно полно теория и методы рентгеноструктурного анализа изложены в [9-11].

Вместо рентгеновских лучей для целей структурного и фазового анализа могут быть использованы и потоки нейтронов или электронов с подходящей длиной волны де-Бройля, задаваемой их кинетической энергией. Эти методы, очень похожие на рентгеновские, но более сложные с технической точки зрения, получившие названия нейтронографии и электронографии изложены в [12, 7].

Электроны, движущиеся в кристалле и являющиеся его "собственностью", также способны к дифракции на кристаллической решетке этого же кристалла. Дифракция этих электронов (при выполнении условий дифракции

) обуславливает особенности процессов переноса заряда и тепла в кристаллах, а также особенности распределения энергетических уровней электронов в кристаллах, рассмотренные в последующих главах и, в частности, деление веществ на проводники, полупроводники и диэлектрики.