В данном разделе рассмотрены простейшие случаи теоретического построения зависимости частоты фононов от их волнового вектора, называемой дисперсионной зависимостью фонона. В общем случае эта задача - очень сложна и решается как правило численными методами.
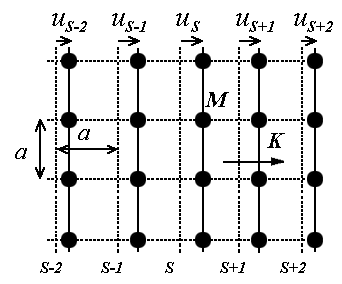
Случай одноатомной ячейки. Рассмотрим для простоты кубический кристалл с примитивной элементарной ячейкой с периодом 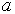 с базисом, состоящим из одного атома. В этом кристалле рассмотрим направление [100] и плоскую продольную волну (случай поперечной волны рассматривается подобным же образом), распространяющуюся вдоль этого направления (см. рис. 3.5).
с базисом, состоящим из одного атома. В этом кристалле рассмотрим направление [100] и плоскую продольную волну (случай поперечной волны рассматривается подобным же образом), распространяющуюся вдоль этого направления (см. рис. 3.5).
|
| Рис. 3.5. Колебания атомов одноатомной кубической решетки в продольной плоской волне, распространяющейся вдоль направления [100] |
В таком случае атомы, расположенные в одной плоскости (100) с номером  , будут смещаться на величину
, будут смещаться на величину  с одной фазой вдоль нормали к этой плоскости (вдоль [100]), то есть вся плоскость атомов будет колебаться как целое. На выбранный атом в этой плоскости с номером
с одной фазой вдоль нормали к этой плоскости (вдоль [100]), то есть вся плоскость атомов будет колебаться как целое. На выбранный атом в этой плоскости с номером 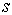 будет действовать другая плоскость с номером
будет действовать другая плоскость с номером 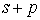 силой
силой 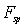 . В случае малых смещений
. В случае малых смещений 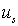 можно предположить, что эта сила пропорциональна разности смещений
можно предположить, что эта сила пропорциональна разности смещений 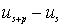 взаимодействующих плоскостей от их положения равновесия. Результирующая сила
взаимодействующих плоскостей от их положения равновесия. Результирующая сила 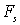 будет суммой сил
будет суммой сил 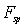 :
:
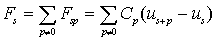 . .
| (3.5) |
Запишем второй закон Ньютона для атома с массой 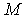 , находящегося на плоскости с номером
, находящегося на плоскости с номером 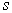 :
:
 . .
| (3.6) |
Будем искать функцию 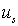 в виде плоской продольной волны:
в виде плоской продольной волны:
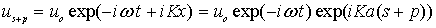 . .
| (3.7) |
После подстановки 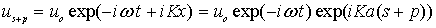
в 
и сокращения общих сомножителей получим выражение для 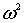 :
:
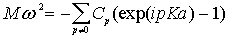 . .
| (3.8) |
С учетом симметрии рассматриваемой решетки 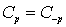 и соотношения
и соотношения 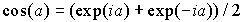 получаем выражение:
получаем выражение:
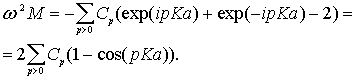
| (3.9) |
Часто ограничиваются рассмотрением взаимодействия выделенного атома только с ближайшими плоскостями. Тогда 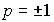 , и выражение для
, и выражение для 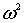 упрощается:
упрощается:
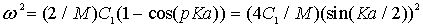 . .
| (3.10) |
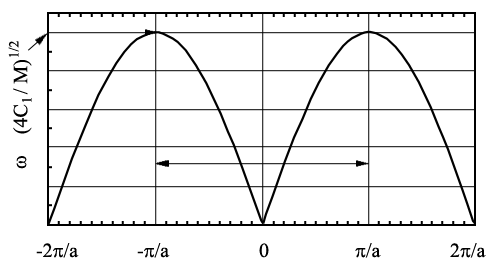
График зависимости 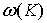 приведен на рис. 3.6. Видно, что в точке
приведен на рис. 3.6. Видно, что в точке 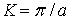 , соответствующей границе первой зоны Бриллюэна, производная
, соответствующей границе первой зоны Бриллюэна, производная 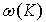 по
по 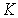 равна нулю, что соответствует равенству нулю групповой скорости фонона.
равна нулю, что соответствует равенству нулю групповой скорости фонона.
|
Рис. 3.6. Зависимость частоты (от волнового вектора 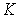 для случая продольной плоской волны, распространяющейся вдоль направления [100] в примитивной кубической решетке для случая продольной плоской волны, распространяющейся вдоль направления [100] в примитивной кубической решетке
|
Такая же особенность зависимости 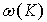 следует и из
следует и из 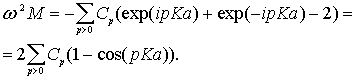
, учитывающей взаимодействие с выбранным атомом нескольких атомных плоскостей. В случае 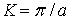 в соответствии с
в соответствии с 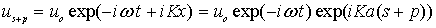
соседние атомы будут двигаться в противофазе, что соответствует стоячей волне с пучностями в местах расположения атомов. Образование стоячей волны в этом случае связано с отражением волны от каждого из атомов и интерференционным усилением отраженных волн. В самом деле, условие усиления волн, отраженных от атомов, расположенных на расстоянии 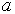 , (см. рис. 3.5) имеет вид
, (см. рис. 3.5) имеет вид 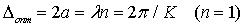 , откуда
, откуда 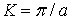 .
.
В случае трехмерной решетки фононы способны отражаться и от атомных плоскостей подобно рентгеновским лучам; условие интерференционного усиления примет в этом случае вид уравнения Вульфа-Брегга. Это условие, согласно рассмотрению в главе 1, идентично попаданию волнового вектора фонона на границу зоны Бриллюэна.
Заметим, что при описании колебаний атомов в волне формулой 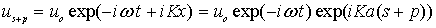
закон движения атомов получается одинаковым, если к величине 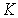 прибавлять или отнимать величину
прибавлять или отнимать величину 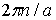 , равную вектору обратной решетки. Поэтому для описания движений атомов в нашем простом случае достаточно использовать значения
, равную вектору обратной решетки. Поэтому для описания движений атомов в нашем простом случае достаточно использовать значения 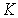 , удовлетворяющие условию
, удовлетворяющие условию 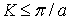 . В трехмерном случае этому условию удовлетворяют
. В трехмерном случае этому условию удовлетворяют 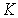 , лежащие внутри первой зоны Бриллюэна.
, лежащие внутри первой зоны Бриллюэна.
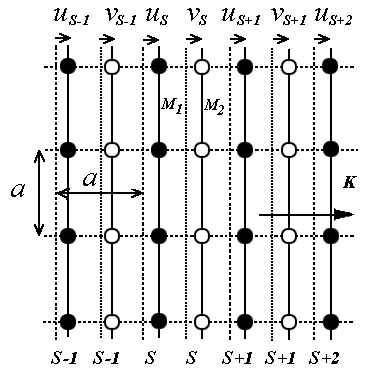
Колебания атомов в ячейке с базисом из двух атомов. Рассмотрим для простоты изложения кубический кристалл с примитивной элементарной ячейкой с периодом 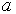 и с базисом, состоящим из двух атомов (рис. 3.7). Пусть атомы имеют массы
и с базисом, состоящим из двух атомов (рис. 3.7). Пусть атомы имеют массы 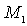 и
и 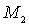 .
.
|
| Рис. 3.7. Колебания атомов кубической решетки с базисом из двух атомов в продольной плоской волне, распространяющейся вдоль направления [100] |
В этом кристалле рассмотрим направление [100] и плоскую продольную волну (случай поперечной волны рассматривается подобным же образом), распространяющуюся вдоль этого направления. В таком случае зачерненные на рис. 3.7 атомы с массой 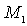 , расположенные в одной плоскости (100) с номером
, расположенные в одной плоскости (100) с номером 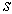 , будут смещаться на величину
, будут смещаться на величину 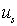 с одной фазой вдоль нормали к этой плоскости (вдоль направления [100]), то есть вся плоскость атомов будет колебаться как целое. Аналогично светлые атомы (см. рис. 3.7) с массой
с одной фазой вдоль нормали к этой плоскости (вдоль направления [100]), то есть вся плоскость атомов будет колебаться как целое. Аналогично светлые атомы (см. рис. 3.7) с массой 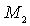 , расположенные в одной плоскости с номером
, расположенные в одной плоскости с номером 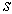 ,будут смещаться на величину
,будут смещаться на величину 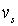 с одной фазой вдоль нормали к этой плоскости вдоль [100], то есть вся плоскость атомов будет также колебаться как целое. Сделаем важное дополнительное упрощение: предположим, что на один выбранный атом в плоскости с номером
с одной фазой вдоль нормали к этой плоскости вдоль [100], то есть вся плоскость атомов будет также колебаться как целое. Сделаем важное дополнительное упрощение: предположим, что на один выбранный атом в плоскости с номером 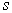 будут действовать только атомы двух ближайших плоскостей.
будут действовать только атомы двух ближайших плоскостей.
В случае малых смещений 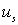 и
и 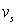 можно предположить, что сила, действующая со стороны атомов ближайших плоскостей, пропорциональна разности смещений
можно предположить, что сила, действующая со стороны атомов ближайших плоскостей, пропорциональна разности смещений 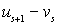 и
и 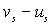 (для светлых атомов) и
(для светлых атомов) и 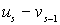 и
и 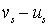 (для темных атомов) ближайших плоскостей от их положения равновесия.
(для темных атомов) ближайших плоскостей от их положения равновесия.
Запишем второй закон Ньютона для "темного" и "светлого" атома (см. рис. 3.7) плоскости с номером 
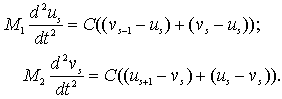
| (3.11) |
Будем искать функции 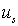 и
и 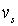 в виде плоской продольной волны:
в виде плоской продольной волны:
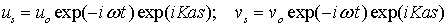
| (3.12) |
После подстановки 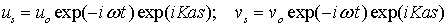
в 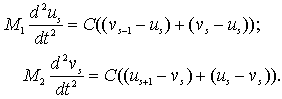
получим систему двух линейных однородных уравнений относительно 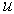 и
и 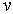 :
:
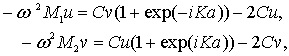
| (3.13) |
которая имеет ненулевое решение, если ее определитель равен нулю.
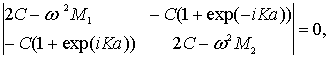
| (3.14) |
Уравнение 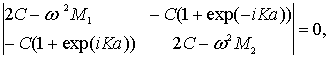
можно, расписать в виде:
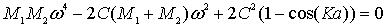 . .
| (3.15) |
Результаты решения уравнения 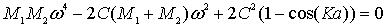
при произвольных 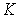 приведены на рис. 3.8.
приведены на рис. 3.8.
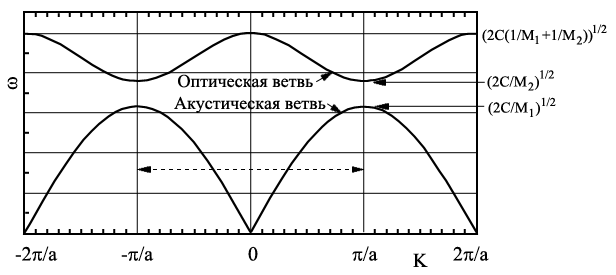
|
Рис. 3.8. Зависимость частоты 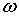 от волнового вектора от волнового вектора 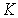 для случая продольной плоской волны, распространяющейся вдоль направления [100] в кубической решетке с базисом из двух атомов. для случая продольной плоской волны, распространяющейся вдоль направления [100] в кубической решетке с базисом из двух атомов.
|
Наибольший "методический" интерес представляет решение этого уравнения в случаях: 1)малых 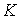 и 2) вблизи значения
и 2) вблизи значения 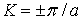 .
.
В случае малых 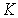 значение
значение 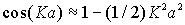 . Тогда уравнение
. Тогда уравнение 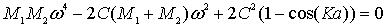
имеет два корня:
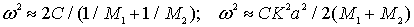 . .
| (3.16) |
Первый корень соответствует оптической ветви дисперсионной зависимости фонона 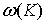 , а второй корень соответствует акустической ветви дисперсионной зависимости фонона
, а второй корень соответствует акустической ветви дисперсионной зависимости фонона 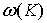 .
.
Для оптической ветви из 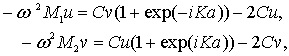
следует, что атомы колеблются приблизительно в противофазе, а именно при 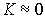 выполняется соотношение:
выполняется соотношение: 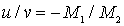 . Такой вид колебаний (см. рис. 3.9 б) можно возбуждать переменным электрическим полем электромагнитной волны в случае разных зарядов атомов 1 и 2; отсюда и появилось название "оптический фонон". Заметим что действием магнитного поля в рассмотренном случае пренебрегают, поскольку магнитное поле волны при малых скоростях движения, согласно законам электродинамики, значительно слабее воздействует на заряды.
. Такой вид колебаний (см. рис. 3.9 б) можно возбуждать переменным электрическим полем электромагнитной волны в случае разных зарядов атомов 1 и 2; отсюда и появилось название "оптический фонон". Заметим что действием магнитного поля в рассмотренном случае пренебрегают, поскольку магнитное поле волны при малых скоростях движения, согласно законам электродинамики, значительно слабее воздействует на заряды.
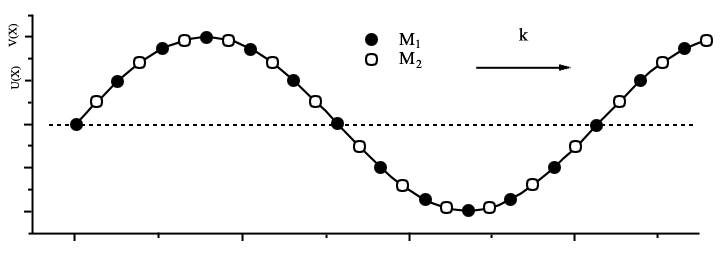
|
| Рис. 3.9а. Отклонения атомов в случае акустического (а) и оптического (б) типов поперечных колебаний атомов |
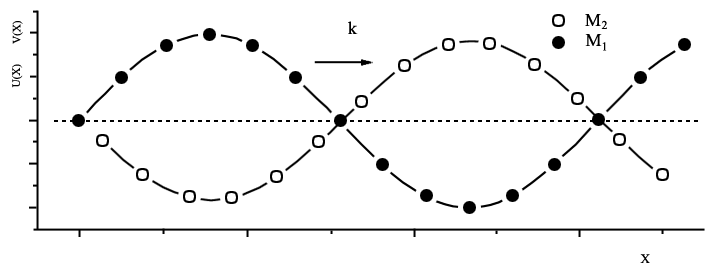
|
| Рис. 3.9б. Отклонения атомов в случае акустического (а) и оптического (б) типов поперечных колебаний атомов |
Для акустической ветви из 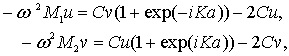
следует, что атомы колеблются приблизительно в одной фазе, а именно при 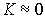 выполняется соотношение:
выполняется соотношение: 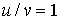 . Такой вид колебаний (см. рис. 3.9 а) можно возбуждать переменным упругим воздействием на кристалл. Он соответствует акустическим колебаниям атомов в длинноволновом приближении сплошной среды, когда атомы движутся согласованно приблизительно в одной фазе; отсюда и появилось название "акустический фонон".
. Такой вид колебаний (см. рис. 3.9 а) можно возбуждать переменным упругим воздействием на кристалл. Он соответствует акустическим колебаниям атомов в длинноволновом приближении сплошной среды, когда атомы движутся согласованно приблизительно в одной фазе; отсюда и появилось название "акустический фонон".
Интересен случай когда 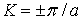 . В этом случае уравнение
. В этом случае уравнение 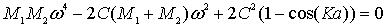
сильно упрощается и для 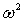 получаются два корня:
получаются два корня: 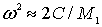 или
или 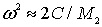 . На рис. 3.8 видно, что при
. На рис. 3.8 видно, что при 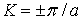 больший корень попадает на оптическую ветвь, а меньший - на акустическую.
больший корень попадает на оптическую ветвь, а меньший - на акустическую.
Видно, что существует область 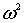 , где нет решений уравнения
, где нет решений уравнения 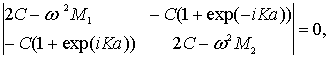
, а значит волна не может распространяться в кристалле с двухатомной элементарной ячейкой. Более детальный анализ показывает, что решения уравнения 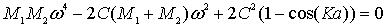
для этой области частот отвечают комплексным значениям 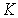 . Это соответствует быстрому уменьшению амплитуды волны в среде. Подробнее эти вопросы рассмотрены в [1].
. Это соответствует быстрому уменьшению амплитуды волны в среде. Подробнее эти вопросы рассмотрены в [1].
Колебания атомов в многоатомной решетке - можно рассмотреть по той же схеме, что и двухатомной. Однако такое рассмотрение намного труднее с математической точки зрения (потребуется решать большее число уравнений, определитель 
однородной системы будет большего порядка, и т.д.). В результате в случаях, аналогичных рассмотренным выше, для ячейки, содержащей  атомов, получаются
атомов, получаются 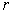 корней уравнения типа
корней уравнения типа 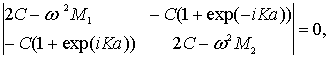
как для продольной, так и для поперечной волны; часть из них принято считать отвечающим акустической ветви, а другую часть - оптической ветви зависимости 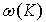 . Всего получаются три акустические ветви и
. Всего получаются три акустические ветви и 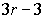 оптические ветви зависимости
оптические ветви зависимости 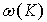 , а в сумме -
, а в сумме - 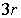 ветвей фононного спектра.
ветвей фононного спектра.
 2020-10-12
2020-10-12 316
316








