2020-10-12
116
Запишем вектор-функцию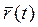 
в форме (1): 
. Тогда скорость точки P будет иметь вид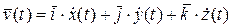 
, где точкой обозначаются полные производные по времени t, т.е. 
, 
, 
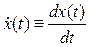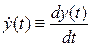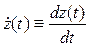. Эти производные координат вектора 
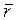имеют геометрический смысл проекций вектора 
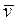на оси Ox, Oy и Oz.
Величина скорости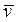 
определяется равенством
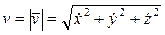, (5)
а направление вектора 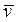относительно осей Ox, Oy и Oz – направляющими косинусами [1]
, 
, 
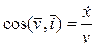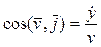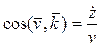. (6)
Ускорение точки P определяется равенством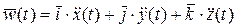 
, где двумя точками обозначены вторые производные по времени t: 
, 
, 
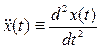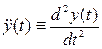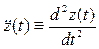. Эти производные координат вектора 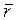имеют геометрический смысл проекций вектора 
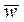на оси Ox, Oy и Oz. Величина вектора ускорения и его направления определяются равенствами, аналогичными (5), (6). Таким образом, движение точки будет полностью заданным, если известны законы изменения ее координат: 
.
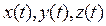Задача
Задан закон движения точки P: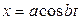 
, 
, 
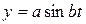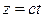, где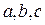 
- постоянные. Найти траекторию, скорость и ускорение точки.
Решение
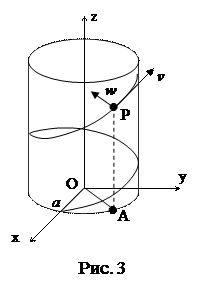
Возведя в квадрат первые равенства, и сложив их, получим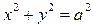 
. Это показывает, что точка P движется по поверхности цилиндра радиуса a, ось которого совпадает с осью Oz (рис. 3). Пусть φ – угол между проекцией OA радиус-вектора OP на плоскость Oxy и осью Ox. Тогда 
, 
, 
, 
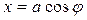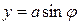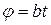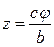. Следовательно, отрезок OA равномерно вращается, а точка P равномерно перемещается по образующей AP. Таким образом, точка движется по винтовой линии.
Определим скорость точки P: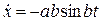 
, 
, 
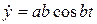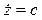. Модуль скорости 
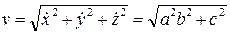, т.е. величина вектора скорости постоянна, а ее направление изменяется со временем.
Ускорение точки P: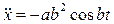 
, 
, 
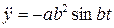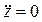. Модуль ускорения 
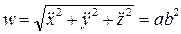. Направляющие косинусы вектора ускорения 
, 
, 
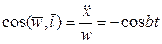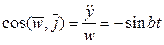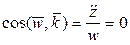. Следовательно, ускорение точки P имеет постоянную величину и направлено по внутренней нормали цилиндра (рис. 3).
 | |||||
 | |||||
| |||||
