Можно задать движение точки P, заранее определив ее траекторию σ относительно точки O. Тогда, на известной траектории выбирается начало отсчета дуговой координаты σ(t) точка O1 и положительное направление отсчета положения точки P (рис. 4). Такой способ задания движения точки называется естественным.
Для вычисления скорости и ускорения точки P при естественном способе задания движения введем правую тройку единичных векторов  . Вектор
. Вектор 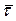 направлен по касательной к траектории в точке P, вектор
направлен по касательной к траектории в точке P, вектор 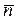 - по нормали. Вектор
- по нормали. Вектор 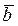 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов  . Радиус-вектор точки P относительно точки O будет сложной функцией времени:
. Радиус-вектор точки P относительно точки O будет сложной функцией времени:  . Тогда скорость точки P будет определяться равенством
. Тогда скорость точки P будет определяться равенством
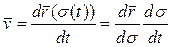 . (7)
. (7)
Вычислим производную 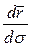 . Она равна
. Она равна 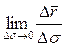 . Ясно, что при
. Ясно, что при  длина хорды
длина хорды 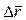 будет приближаться к длине соответствующей дуги
будет приближаться к длине соответствующей дуги  и
и 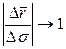 . При этом
. При этом 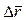 займет положение касательной к σ в точке P. Следовательно,
займет положение касательной к σ в точке P. Следовательно,  и равенство (7) запишется в виде
и равенство (7) запишется в виде
 . (8)
. (8)
Равенство (8) показывает, что скорость точки P всегда направлена по касательной к траектории. Ускорение точки P, с учетом (8), имеет вид
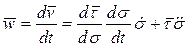 . (9)
. (9)
Вычислим производную  =
=  . Ясно, что единичный вектор
. Ясно, что единичный вектор 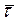 изменяется только по направлению при движении точки P по траектории σ. Приращение дуги представим в виде
изменяется только по направлению при движении точки P по траектории σ. Приращение дуги представим в виде 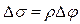 , где ρ – радиус кривизны траектории, Δφ – приращение угла поворота радиуса кривизны. Тогда можно записать
, где ρ – радиус кривизны траектории, Δφ – приращение угла поворота радиуса кривизны. Тогда можно записать 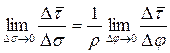 . При
. При 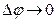 длина
длина 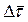 будет приближаться к величине угла
будет приближаться к величине угла 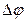 и
и 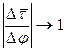 . При этом
. При этом 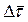 займет положение нормали к σ в точке P. Следовательно,
займет положение нормали к σ в точке P. Следовательно, 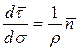 и равенство (9) запишется в виде
и равенство (9) запишется в виде
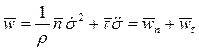 . (10)
. (10)
Соотношение (10) называется теоремой о разложении полного ускорения точки на нормальную  и тангенциальную
и тангенциальную 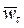 составляющие. Нормальное ускорение
составляющие. Нормальное ускорение  точки объясняется наличием кривизны траектории и характеризует изменение вектора скорости точки P по направлению. Тангенциальное ускорение
точки объясняется наличием кривизны траектории и характеризует изменение вектора скорости точки P по направлению. Тангенциальное ускорение 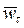 характеризует изменение вектора скорости точки P по величине. Если траектория точки – кривая, то в любом случае
характеризует изменение вектора скорости точки P по величине. Если траектория точки – кривая, то в любом случае  и вектор полного ускорения
и вектор полного ускорения 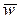 будет всегда направлен внутрь траектории.
будет всегда направлен внутрь траектории.
Задача
Точка P движется по окружности радиуса R, закон движения точки  . Определить модуль полного ускорения точки и угол между полным ускорением и его нормальной составляющей.
. Определить модуль полного ускорения точки и угол между полным ускорением и его нормальной составляющей.
Решение
Так как 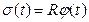 , из (8) и (10) следует, что
, из (8) и (10) следует, что 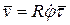 ,
, 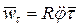 ,
, 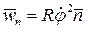 . Величины
. Величины  и
и 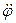 являются соответственно угловой скоростью и угловым ускорением радиуса OP = R (рис. 5). Обозначая
являются соответственно угловой скоростью и угловым ускорением радиуса OP = R (рис. 5). Обозначая 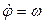 ,
, 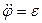 , получим выражение для модуля ускорения точки:
, получим выражение для модуля ускорения точки:
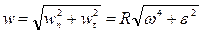 .
.
 Угол между полным ускорением и его нормальной составляющей определяется из равенства
Угол между полным ускорением и его нормальной составляющей определяется из равенства 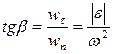 .
.
 | ||||||
| ||||||
| ||||||
 2020-10-12
2020-10-12 191
191








