2020-10-12
134
Если точка P движется в заданной плоскости, то, помимо декартовых координат x(t) и y(t) движение может быть задано законами изменения длины радиус-вектора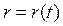 
и угла его поворота в плоскости 
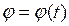(рис 6). Такую систему координат называют полярной. Единичные векторы 
и 
задают направления двух взаимно перпендикулярных осей: радиальной и трансверсальной соответственно. Проекции вектора скорости точки P на эти оси называются соответственно радиальной и трансверсальной скоростями:
, 
. (11)
Для проекций ускорения точки P
, 
. (12)
Связь между декартовыми и полярными координатами выражается соотношениями: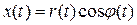 
, 
.
Задача
Движение точки P задано уравнениями: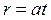 
, 
, 
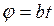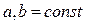. Найти траекторию, скорость и ускорение точки.
Решение
Исключив из данных уравнений время t, получим уравнение траектории 
. Эта линия называется спиралью Архимеда. Согласно (11) имеем
, 
.
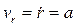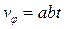Величина скорости точки P: 
. Согласно (12) имеем
, 
.
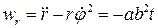Величина ускорения точки P: 
.
Вопросы для проверки усвоения материала
1) Сформулируйте задачу кинематики точки.
2) Что такое радиус-вектор положения точки?
3) Перечислите способы задания движения точки.
4) Дайте определения скорости и ускорения точки.
5) Как направлена скорость точки?
6) Сформулируйте теорему о разложении полного ускорения точки.
7) Почему ускорение точки всегда направлено внутрь траектории?
8) Какую систему координат называют полярной?
9) Как направлены радиальная и трансверсальная оси?
10) Как связаны между собой декартовая и полярная системы координат?
