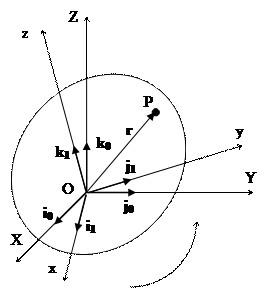
Рассмотрим твердое тело, вращающееся вокруг точки O (рис. 9). Система координат OXYZ – неподвижная, а Oxyz – жестко связана с вращающимся твердым телом и потому является подвижной. Направления осей этих систем координат задаются соответствующими тройками единичных векторов 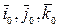 и
и 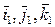 . Пусть известно положение точки P в системе координат Oxyz:2
. Пусть известно положение точки P в системе координат Oxyz:2
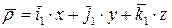 .
.
Вычислим положение точки P в неподвижной системе координат OXYZ. Для этого спроецируем вектор 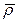 на оси OX, OY и OZ:
на оси OX, OY и OZ:
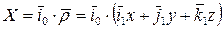 ,
,
 ,
,
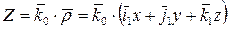 .
.
Полученные соотношения связывают положение точки P в неподвижной и подвижной системах координат. Запишем эти соотношения в матричной форме:
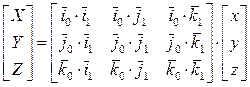 ,
,
или, окончательно,
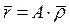 . (1)
. (1)
 | |||||||
 | |||||||
| |||||||
| |||||||
Матрица A в формуле (1) называется матрицей поворота. Она является ортогональной, т.е.  .3 Ее определитель по абсолютной величине всегда равен единице. Элементами матрицы A являются косинусы углов между осями неподвижной и подвижной систем координат:
.3 Ее определитель по абсолютной величине всегда равен единице. Элементами матрицы A являются косинусы углов между осями неподвижной и подвижной систем координат:
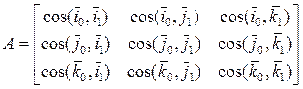 .
.
В общем случае матрица A задает перемещение твердого тела вокруг произвольной оси, проходящей через точку O. Повороты твердого тела вокруг неподвижных осей OX, OY и OZ называют элементарными, а соответствующие им матрицы
 ,
, 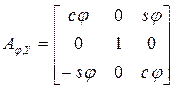 ,
, 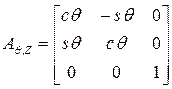
матрицами элементарных поворотов. 4 Обозначения читаются так: 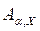 - матрица поворота вокруг оси OX на угол α. Матрица поворота твердого тела вокруг неподвижной точки может быть представлена в виде произведения матриц элементарных поворотов, например:
- матрица поворота вокруг оси OX на угол α. Матрица поворота твердого тела вокруг неподвижной точки может быть представлена в виде произведения матриц элементарных поворотов, например:
 ,
,
т.е. твердое тело сначала поворачивается вокруг оси OX на угол α, затем вокруг оси OY на угол φ, и еще вокруг оси OZ на угол θ. Изменение порядка умножения матриц элементарных поворотов в общем случае приведет к изменению матрицы результирующего поворота, т.к. произведение матриц не обладает свойством коммутативности (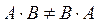 ). Если определить матрицу поворота как функцию времени A = A(t), то будет задано движение твердого тела вокруг неподвижной точки:
). Если определить матрицу поворота как функцию времени A = A(t), то будет задано движение твердого тела вокруг неподвижной точки: 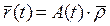 .
.
Задача
В неподвижной системе координат OXYZ заданы радиус-векторы концов тонкого стержня AB: 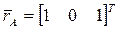 ,
,  . Определить положение стержня после его поворота вокруг оси OZ на угол θ = 600.
. Определить положение стержня после его поворота вокруг оси OZ на угол θ = 600.
Решение
Введем систему координат Oxyz, жестко связанную со стержнем. Пусть начальное положение этой системы координат совпадает с положением осей неподвижной системы координат OXYZ. Тогда радиус-векторы точек A и B в этих системах координат будут совпадать:  ,
, 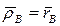 . Положение стержня после указанного поворота определится из соотношений:
. Положение стержня после указанного поворота определится из соотношений:
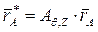 ,
, 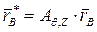 .
.
Выполняя вычисления, получим:
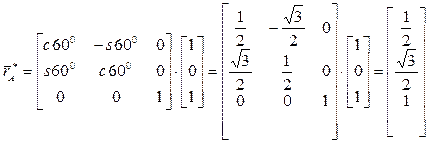 ;
;
 .
.
Начальное и конечное положения стержня приведены на рис. 10.
 2020-10-12
2020-10-12 271
271








