Твердые тела, входящие в состав механизмов и машин, не могут двигаться произвольно. Их движения ограничиваются за счет контакта в подвижных соединениях механизма и, как правило, представляют собой следующие частные случаи: вращение вокруг неподвижной оси и плоское движение.
Вращение вокруг неподвижной оси
Формулы для скорости и ускорения точки P твердого тела, вращающегося вокруг неподвижной оси OZ, получаются из общих соотношений (3) и (5) путем применения к этим соотношениям частных условий:
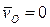 ,
,  ,
,  .
.
В результате из (3) следует
 ,
,  , (6)
, (6)
а из (5)
 ,
,
 ,
, 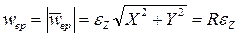 ;
;
 ,
, 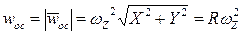 . (7)
. (7)
Таким образом, любая точка твердого тела, не лежащая на оси его вращения, движется по окружности радиуса R в плоскости, перпендикулярной оси вращения (рис.15). Формулы (6), (7) соответствуют случаю движения точки по окружности6.
Плоское движение
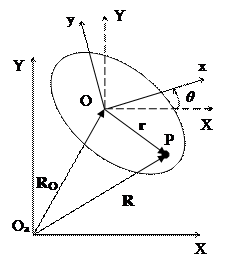
Движение твердого тела называется плоским, если все точки тела движутся в плоскостях, параллельных неподвижной плоскости.
 | |||||
 | |||||
| |||||
Плоское движение твердого тела эквивалентно движению соответствующей плоской фигуры в собственной плоскости (рис. 16). Фигура имеет свободу по трем независимым перемещениям: вдоль оси OaX, вдоль оси OaY и вращение в плоскости OaXY. Соответственно, любое положение фигуры может быть задано тремя координатами: XO, YO, θ.
Формулы для скорости и ускорения точки P твердого тела, совершающего плоское движение, получаются из общих соотношений (3) и (5) путем применения к этим соотношениям частных условий:
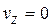 ,
,  ,
,  .
.
В результате из (3) следует7
 , (8)
, (8)
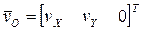 ,
,  ,
, 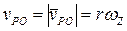 ,
,
а из (5)
 , (9)
, (9)
 ,
, 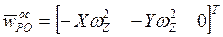 ,
, 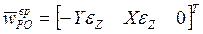 ,
,
 ,
, 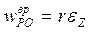 .
.
Таким образом, в случае плоского движения, векторы скорости и ускорения точки твердого тела всегда лежат в плоскости движения, а векторы угловой скорости и углового ускорения всегда перпендикулярны этой плоскости. Этот факт позволяет при решении практических задач оперировать линейными скоростями и ускорениями как векторами в плоскости, а угловыми скоростями и ускорениями – как скалярными величинами.
Задача
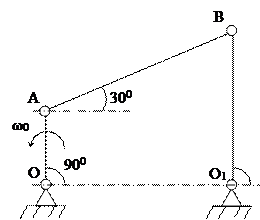
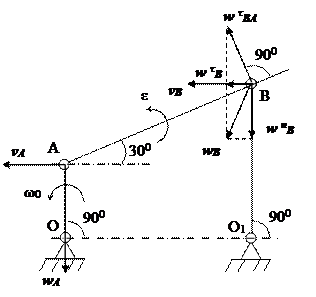 Стержень OA шарнирного четырехзвенника (рис. 17) вращается с постоянной угловой скоростью ω0. Определить угловую скорость, угловое ускорение стержня AB, а также ускорение шарнира B в положении, указанном на рисунке, если AB = 2OA = 2a.
Стержень OA шарнирного четырехзвенника (рис. 17) вращается с постоянной угловой скоростью ω0. Определить угловую скорость, угловое ускорение стержня AB, а также ускорение шарнира B в положении, указанном на рисунке, если AB = 2OA = 2a.
 | |||||
| |||||
| |||||
Решение
Стержень AB изображенного на рисунке четырехзвенного механизма совершает плоское движение, а стержни OA и O1B вращаются вокруг неподвижных центров O и O1. Найдем скорость шарнира A:
 .
.
Вектор  перпендикулярен OA и направлен в сторону вращения стержня OA (рис. 18). Для скорости шарнира B справедливо равенство (8):
перпендикулярен OA и направлен в сторону вращения стержня OA (рис. 18). Для скорости шарнира B справедливо равенство (8):
 ,
,
причем направление  , согласно положению механизма, будет то же, что и у
, согласно положению механизма, будет то же, что и у  . Из этого следует, что
. Из этого следует, что 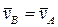 ,
,  ,
,  , т.е. стержень AB совершает мгновенно-поступательное движение.
, т.е. стержень AB совершает мгновенно-поступательное движение.
Найдем ускорение шарнира A. Так как этот шарнир движется вокруг неподвижной точки O, то для его ускорения справедливо равенство (7):
 ,
,
где  - нормальное ускорение, направленное от точки A к центру вращения O;
- нормальное ускорение, направленное от точки A к центру вращения O; 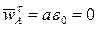 , т.к.
, т.к.  . В данном случае
. В данном случае 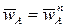 . Для ускорения шарнира B справедливо равенство (9):
. Для ускорения шарнира B справедливо равенство (9):
 , (10)
, (10)
где 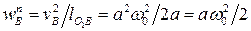 - нормальное ускорение шарнира B в его движении вокруг неподвижной точки O1;
- нормальное ускорение шарнира B в его движении вокруг неподвижной точки O1;  - нормальное ускорение шарнира B относительно точки A.
- нормальное ускорение шарнира B относительно точки A.
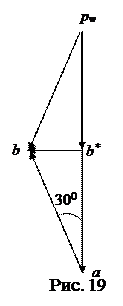
Неизвестные по величине векторы  определим, построив план ускорений. Для этого из произвольной точки pw, называемой полюсом плана ускорений, отложим отрезок pwa,, отображающий ускорение
определим, построив план ускорений. Для этого из произвольной точки pw, называемой полюсом плана ускорений, отложим отрезок pwa,, отображающий ускорение 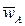 (рис. 19). Тогда, проводя через точку a прямую, перпендикулярную AB, получим направление тангенциального ускорения
(рис. 19). Тогда, проводя через точку a прямую, перпендикулярную AB, получим направление тангенциального ускорения  . Составляющую результирующего ускорения
. Составляющую результирующего ускорения 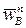 отложим из полюса pw в виде отрезка pwb*, длина которого вдвое меньше pwa. Замкнем план ускорений прямой, перпендикулярной стержню O1B и задающей направление
отложим из полюса pw в виде отрезка pwb*, длина которого вдвое меньше pwa. Замкнем план ускорений прямой, перпендикулярной стержню O1B и задающей направление  . На пересечении двух перпендикуляров получим точку b. Отрезок pwb будет отображать ускорение
. На пересечении двух перпендикуляров получим точку b. Отрезок pwb будет отображать ускорение 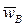 шарнира B, а отрезок ab – ускорение
шарнира B, а отрезок ab – ускорение 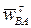 . План ускорений графически отображает векторное равенство (10), из плана легко определяются все неизвестные ускорения:
. План ускорений графически отображает векторное равенство (10), из плана легко определяются все неизвестные ускорения:
 | |||
 | |||
 - ускорение шарнира B;
- ускорение шарнира B;
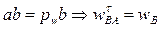 ,
, 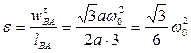 - угловое ускорение стержня AB. Направления всех вычисленных скоростей и ускорений точек механизма изображены на рис. 18.
- угловое ускорение стержня AB. Направления всех вычисленных скоростей и ускорений точек механизма изображены на рис. 18.
В задачах на случай плоского движения твердого тела иногда удается получить более короткое решение за счет использования понятий мгновенный центр скоростей и мгновенный центр ускорений. Мгновенным центром скоростей (МЦС) называют такую точку плоской фигуры, скорость которой в данный момент времени движения равна нулю. Скорости остальных точек фигуры при этом такие, какие они были бы при вращательном движении фигуры вокруг МЦС. Мгновенный центр ускорений (МЦУ), соответственно, это такая точка плоской фигуры, ускорение которой в данный момент времени движения равно нулю. Ускорения остальных точек фигуры такие, какие они были бы при ее вращательном движении относительно МЦУ.
Решим предыдущую задачу, используя понятия МЦС и МЦУ. Из рис. 17 видно, что стержень OA параллелен стержню O1B. Следовательно, абсолютные скорости точек A и B стержня AB параллельны. Учитывая, что в силу неизменности расстояния между точками A и B проекции скоростей  и
и  на направление AB должны быть одинаковыми (точка B не может догнать точку A, но также не может отстать от точки A), заключаем, что
на направление AB должны быть одинаковыми (точка B не может догнать точку A, но также не может отстать от точки A), заключаем, что 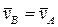 . Таким образом, стержень AB совершает мгновенно-поступательное движение, положение его МЦС бесконечно удалено и
. Таким образом, стержень AB совершает мгновенно-поступательное движение, положение его МЦС бесконечно удалено и  .
.
Определим направление ускорения  точки B в ее движении относительно точки A. Так как угловая скорость стержня AB
точки B в ее движении относительно точки A. Так как угловая скорость стержня AB  , то
, то 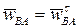 и, следовательно, угол между
и, следовательно, угол между  и AB равен 900 (рис. 20). Согласно определению понятия МЦУ угол между абсолютным ускорением
и AB равен 900 (рис. 20). Согласно определению понятия МЦУ угол между абсолютным ускорением 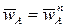 и направлением на МЦУ (точка Q) также равен 900. Для определения положения точки Q воспользуемся соотношением, справедливым при
и направлением на МЦУ (точка Q) также равен 900. Для определения положения точки Q воспользуемся соотношением, справедливым при 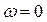 :
:
 . (11)
. (11)
Вычислим ускорение точки A: 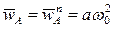 . В силу соотношения
. В силу соотношения  будем иметь
будем иметь  . Так как
. Так как 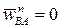 , а
, а  направлено в ту же сторону, что и
направлено в ту же сторону, что и 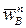 , на основании равенства (10) заключаем:
, на основании равенства (10) заключаем:  (рис. 19). Следовательно, из (11) получим
(рис. 19). Следовательно, из (11) получим  , и точка Q будет симметрична точке A относительно направления O1B (рис. 20). Тогда
, и точка Q будет симметрична точке A относительно направления O1B (рис. 20). Тогда 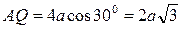 ,
,  и
и  . Угол между
. Угол между  и направлением BQ, согласно определению понятия МЦУ, составит 900.
и направлением BQ, согласно определению понятия МЦУ, составит 900.
 2020-10-12
2020-10-12 277
277








