На план поверхности в масштабе 1:2000 по известным координатам
ХI, YI; XIII, YIII; XIV,YIV наносим пункты опорной сети, исходные данные берем из таблицы 3.1.
Таблица 3.1- Координаты пунктов опорной сети
| Номера пунктов | Х, м | У, м |
| I | 41,61 | 71,61 |
| III | 251,41 | 311,81 |
| IV | 221,71 | 481,21 |
В соответствии с требованиями инструкции, предъявляемые к геодезическим засечками и приведенными выше, выбирается место заложения пункта съемочного обоснования точка P1 .
Для расчета координат точки P1 на исходных пунктах I, II, III измерим углы r1 и r2 в одном треугольнике и r3 и r4 во втором. Дополнительно, для повышения точности расчета, определим значения углов 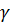 1,
1, 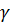 2. Сумма углов в треугольнике уравнивается к
2. Сумма углов в треугольнике уравнивается к 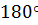 .
.
Координаты пункта Р определяются решением одного треугольника по известным координатам пунктов и измеренным углам.
Известны несколько способов решения прямой засечки. Наиболее распространенные их них два: по формулам котангенсов измеренных углов и тангенсов дирекционных углов. Исходные данные для вычисления координат пункта P1 берем из таблицы 3.2 и 3.3.
Из треугольника I-III-P1.
Таблица3.2-Исходные данные для вычисления координат пункта Р1 из треугольника I
| Вершины | Углы, град. | Х, м | У, м |
| III | 
| 251,41 | 311,81 |
| I | 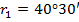
| 41,61 | 71,61 |
| P1 | 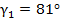 ∑=180 ∑=180 
|
Рассчитываем координаты пункта P1 по формулам Юнга:
Xp= 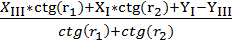 ;
;
Yp= 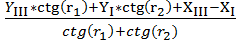 ,
,
где r – углы при пунктах опорной сети;
где X, Y- координаты пунктов опорной сети;
Xp=  м
м
Yp=  м
м
Для контроля рассчитаем координаты пункта I:
X1= 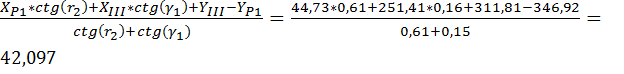 м
м
Y1= 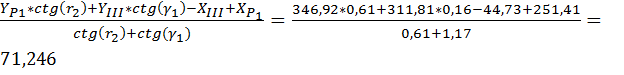 м
м
Из треугольника IV-III-P1.
Таблица 3.3-Исходные данные для вычисления координат пункта Р1
| Вершины | Углы, град. | Х, м | У, м |
| IV | 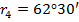
| 221,71 | 481,21 |
| III | 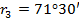
| 251,41 | 311,81 |
| P1 | 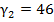 ∑=180°
∑=180°
|
Xp= 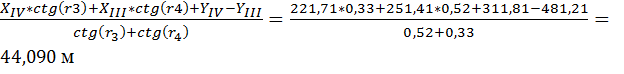 ,
,
Yp= 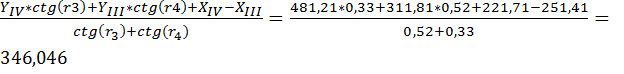 м;
м;
Из решения двух треугольников разница в координатах точки Р1 составляет ∆ХР1=0,641 м, ∆УР1=0,856 м, которая не превышает 0,6 мм на плане в масштабе съемки (1,2 м).
Среднее значение координат точки Р1 из двух треугольников:
ХР1=44,410 м, УР1=346,474 м.
Оценка точности планового положения пункта Р1 характеризуется среднеквадратической погрешностью относительно пунктов опорной сети, величина которой не должна превышать 0,4 мм на плане в масштабе съемки (для масштаба 1:2000 МР ≤0.8 м)
Для треугольника III-I-P1
MP1=± 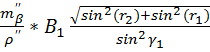 ;
;
Для треугольника IV-III-P1
MP2=± 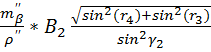 ,
,
где mβ - средняя квадратическая ошибка измерения углов, принимаем mβ=15’’ 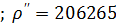 .
.
В1, В2 – базис прямой засечки (расстояние между пунктами опорной сети) определяется решением обратной геодезической задачи.
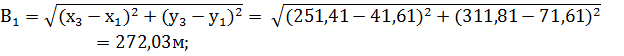
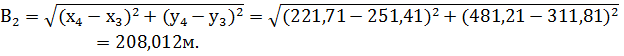
МР1=± 
МР2=±  м.
м.
В результате средняя квадратическая погрешность положения пункта Р1 относительно пунктов опорной сети из двух треугольников составила 0,022 м, что не превышает допустимой величины (0,8 м).
 2020-10-12
2020-10-12 161
161








