2020-10-12
445
Понятие о главном векторе. Основные способы его вычисления
Пусть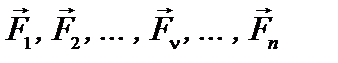 
- произвольная система сил.
Величину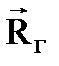 
, определяемую из условия:
К графическому способу вычисления главного вектора 
|
называют главным вектором рассматриваемой системы сил.
| D |
| С |
| 2 |
| А |
| 3 |
обозначим, соответственно,
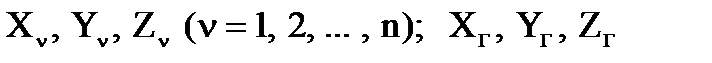. Тогда:
30
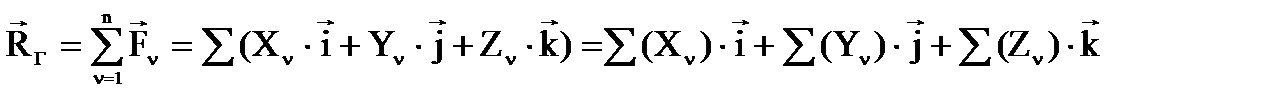Но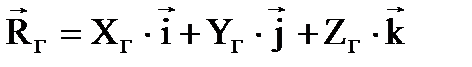 
.
Из сопоставления двух последних выражений:
.
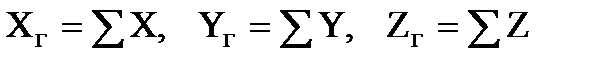Понятие о главном моменте. Аналитический способ его вычисления.
Понятие о главном моменте. Аналитический способ его вычисления
называют «главными моментами заданной системы сил относительно осей соответственно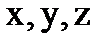 
».
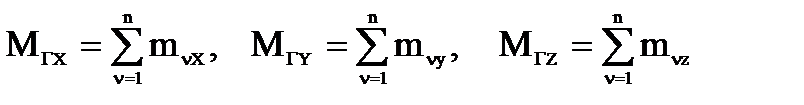, где
- моменты сил заданной системы (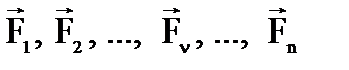
) относительно осей соответственно 
.
ПРИМЕР 12.2. - На вычисление главного момента (аналитическим методом)
Дано: проекции сил 
и координаты точек их приложения определяются из приводимой таблицы
| X, н | Y, н | Z, н | x, м | y, м | z, м |
| 0 | 100 | -60 | 1,0 | 0,0 | 0,0 |
| 100 | 80 | 0 | 0,8 | -0,5 | 0,0 |
| 50 | 0 | 80 | 0,5 | 0,6 | 1,0 |
| -40 | 0 | 0 | 0,4 | 0,0 | -0,8 |
Требуется: определить главный момент заданной системы сил относительно начала координат (который обозначим точкой О).
Решение.
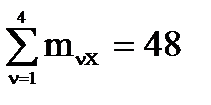Нм.
Аналогично
35
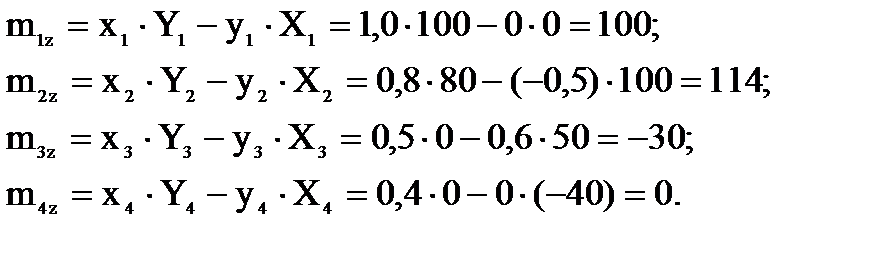
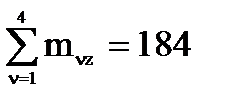Нм.
Нм.
Итак, главный момент заданной системы сил:
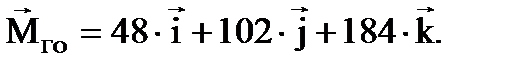
Его модуль:
Нм.
Направляющие косинусы главного момента:
.
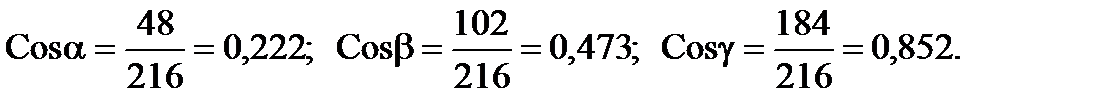Зависимость между главными моментами относительно различных центров.
Зависимость между главными моментами относительно различных центров
Эта зависимость определяется правилами векторной алгебры. На рис.10: О – некий базовый центр (например – начало системы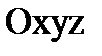 
); А – произвольно взятый другой (новый) центр.
| Рисунок 12.10 |
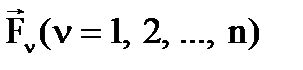получаем:
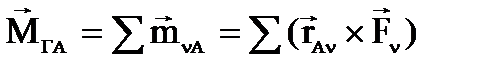
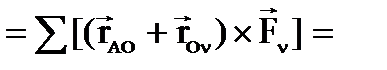
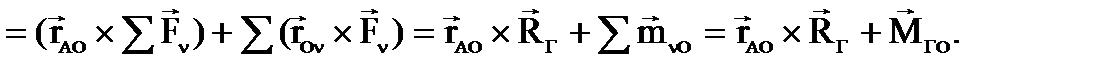
Итак:
-
главный момент произвольной системы сил относительно любого центра А больше главного момента этой же системы относительно ранее взятого центра О на величину, равную векторному произведению радиус-вектора, проведенного из нового центра в старый, на главный вектор
