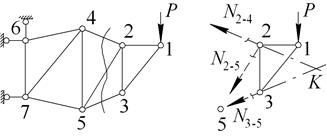
Плоская ферма разрезается на две части таким образом, чтобы в сечение попали не более трёх стержней, в которых усилия ещё не известны (рис. 1.21). Действие одной части на другую заменяется неизвестными усилиями в стержнях. Уравнения равновесия представляются в виде равенства нулю моментов всех сил относительно точек пересечения направлений каждой пары стержней, попавших в сечение. Из уравнений моментов относительно узла 2 определяется усилие 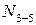 , относительно узла 5 – усилие
, относительно узла 5 – усилие 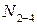 , относительно точки
, относительно точки  (пересечение направлений стержней 2-4 и 3-5) – усилие
(пересечение направлений стержней 2-4 и 3-5) – усилие  .
.
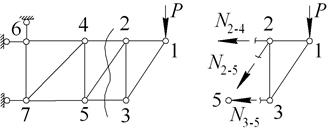
Если два из попавших в сечение стержней параллельны, то одно из уравнений моментов заменяется суммой проекций всех сил на ось, перпендикулярную направлению этих стержней. В представленной на рисунке 1.22 ферме таким образом находится усилие в стержне 2-5.
Преимущество метода моментных точек заключается в том, что каждое уравнение равновесия содержит только одно неизвестное усилие. Но рассмотренные нами фермы относятся к категории простых и, в общем-то, могут быть решены методом вырезания узлов.
|
| Рисунок 1.21 |
|
| Рисунок 1.22 |
Метод замены связей
Это наиболее общий метод решения сложных ферм. Рассмотрим его на примере фермы, представленной на рисунке 1.25. Методом вырезания узлов усилия в стержнях здесь целесообразно определять, так как в каждом узле сходится более двух стержней.
При реализации алгоритма метода замены связей из фермы удаляется один из стержней так, чтобы появились узлы (или узел), присоединённые с помощью двух стержней, не лежащих на одной прямой. Пусть это будет стержень 6-7. Такой стержень называют отброшенным и обозначают его 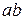 . Затем ферму начинают разбирать, последовательно отсоединяя узлы, прикреплённые с помощью двух стержней, не лежащих на одной прямой. Отбросив стержень
. Затем ферму начинают разбирать, последовательно отсоединяя узлы, прикреплённые с помощью двух стержней, не лежащих на одной прямой. Отбросив стержень 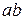 , мы внесли в систему степень свободы (устранили одну связь). В процессе разборки фермы мы обязательно обнаружим её. Снимая узлы рассматриваемой фермы в последовательности 6, 4, 5, 1, мы обнаружим, что теперь стержень 2-3 может вращаться относительно шарнира 3. Чтобы обеспечить неподвижность узла 2, поставим заменяющий стержень
, мы внесли в систему степень свободы (устранили одну связь). В процессе разборки фермы мы обязательно обнаружим её. Снимая узлы рассматриваемой фермы в последовательности 6, 4, 5, 1, мы обнаружим, что теперь стержень 2-3 может вращаться относительно шарнира 3. Чтобы обеспечить неподвижность узла 2, поставим заменяющий стержень 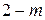 (в нашем случае это опорный стержень, рис. 1.26). Заменяющий стержень будем обозначать
(в нашем случае это опорный стержень, рис. 1.26). Заменяющий стержень будем обозначать 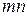 . После этого процесс разборки фермы следует продолжить и убедиться, что она разбирается полностью, то есть является простой и решается методом вырезания узлов. Фактически мы переставили отброшенный стержень в другое место. Полученная таким образом ферма называется преобразованной.
. После этого процесс разборки фермы следует продолжить и убедиться, что она разбирается полностью, то есть является простой и решается методом вырезания узлов. Фактически мы переставили отброшенный стержень в другое место. Полученная таким образом ферма называется преобразованной.
Приложим теперь к узлам 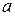 и
и  неизвестные пока силы
неизвестные пока силы 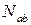 , с которым отброшенный стержень действует на оставшуюся часть.
, с которым отброшенный стержень действует на оставшуюся часть.
Рассмотрим два состояния преобразованной фермы. В одном из них (рисунок 1.26) к ферме приложена только внешняя нагрузка. Усилия в стержнях фермы, соответствующие этому состоянию, будем отмечать сверху индексом «о». Во втором состоянии приложим к узлам 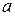 и
и  в направлении отброшенного стержня силы, равные единице, и будем отмечать соответствующие усилия в стержнях чёрточкой сверху. Кроме того, условимся буквой
в направлении отброшенного стержня силы, равные единице, и будем отмечать соответствующие усилия в стержнях чёрточкой сверху. Кроме того, условимся буквой 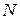 обозначать только усилия в стержнях заданной фермы, а усилия в заменяющем стержне обозначим буквой
обозначать только усилия в стержнях заданной фермы, а усилия в заменяющем стержне обозначим буквой 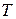 .
.
Пользуясь принципом независимости действия сил, запишем для усилия в заменяющем стержне:
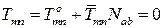 .
.
Здесь  – усилие в заменяющем стержне только от внешней нагрузки,
– усилие в заменяющем стержне только от внешней нагрузки, 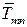 – усилие в заменяющем стержне в единичной системе, а
– усилие в заменяющем стержне в единичной системе, а 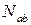 следует понимать как число, показывающее во сколько раз усилие в стержне
следует понимать как число, показывающее во сколько раз усилие в стержне 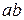 больше единицы. Так как в исходной ферме (рисунок 1.25) стержня
больше единицы. Так как в исходной ферме (рисунок 1.25) стержня 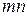 нет, то полное усилие
нет, то полное усилие 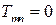 .
.
Последнее равенство можно рассматривать как уравнение относительно 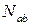 . Тогда получим:
. Тогда получим:
 . (1.5)
. (1.5)
Зная теперь 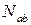 , и пользуясь тем же принципом независимости действия сил, можно определить усилие в произвольном стержне:
, и пользуясь тем же принципом независимости действия сил, можно определить усилие в произвольном стержне:
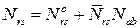 . (1.6)
. (1.6)
Метод замены связей может быть использован и для исследования геометрической неизменяемости системы. Обратимся к формуле (1.5). Если знаменатель правой части отличен от нуля, т.е.  , то для усилия в стержне
, то для усилия в стержне 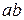 получается конечное, вполне определённое значение. Значит, исходная стержневая система статически определима. Следовательно, она геометрически неизменяема.
получается конечное, вполне определённое значение. Значит, исходная стержневая система статически определима. Следовательно, она геометрически неизменяема.
Если  , то
, то 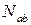 обращается либо в бесконечность, либо в неопределённость. Система при минимально необходимом числе стержней оказывается статически неопределимой. Значит, она геометрически изменяема.
обращается либо в бесконечность, либо в неопределённость. Система при минимально необходимом числе стержней оказывается статически неопределимой. Значит, она геометрически изменяема.
Таким образом, признаком геометрической неизменяемости является отличие от нуля усилия в заменяющем стержне, если в направлении устранённого стержня к узлам фермы приложены силы, равные единице.
|
| Рисунок 1.25 |
Вернёмся теперь к рассматриваемой нами ферме и, в соответствии с алгоритмом метода, проанализируем два состояния преобразованной фермы. На рисунке 1.26а к узлам 6 и 7 в направлении отброшенного стержня приложены единичные силы, а на рисунке 1.26б – внешняя нагрузка. На схемах показаны значения усилий в стержнях, вызванные приложенными силами. Для растянутых стержней стрелки направлены от узла, для сжатых – к узлу.
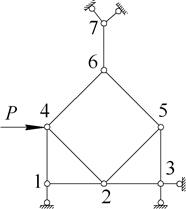
Из рисунка 1.26б видно, что усилие в заменяющем стержне в единичной системе отлично от нуля 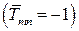 . Следовательно, стержневая система, представленная на рисунке 1.25, геометрически неизменяема.
. Следовательно, стержневая система, представленная на рисунке 1.25, геометрически неизменяема.
|
| Рисунок 1.26 |
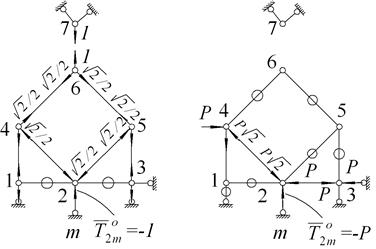
Усилие в заменяющем стержне 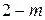 от внешней нагрузки равно
от внешней нагрузки равно 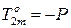 . Для усилия в отброшенном стержне получим:
. Для усилия в отброшенном стержне получим:
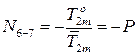 .
.
Можно теперь определить усилия в остальных стержнях фермы. Например, для стержня 2-4 имеем:
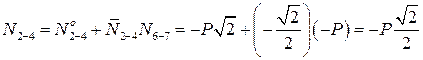 .
.
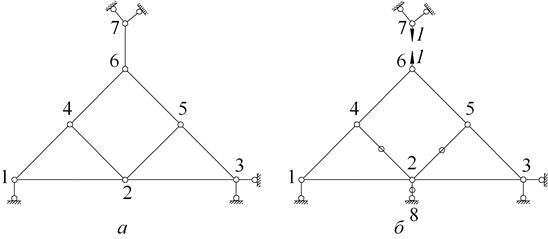
В примере на рисунке 1.27а замена осуществляется, в принципе, так же, как и в предыдущем случае. При определении усилия в заменяющем стержне 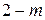 от единичных нагрузок следует учесть, что для узлов 4 и 5 стержни 4-2 и 5-2 отдельно стоящие (рисунок 1.27,б). Поскольку к узлам не приложены внешние силы, усилия в стержнях 4-2 и 5-2 равны нулю. Равно нулю и усилие в заменяющем стержне
от единичных нагрузок следует учесть, что для узлов 4 и 5 стержни 4-2 и 5-2 отдельно стоящие (рисунок 1.27,б). Поскольку к узлам не приложены внешние силы, усилия в стержнях 4-2 и 5-2 равны нулю. Равно нулю и усилие в заменяющем стержне  . Система на рисунке 1.27а статически неопределима и геометрически изменяема.
. Система на рисунке 1.27а статически неопределима и геометрически изменяема.
|
| Рисунок 1.27 |
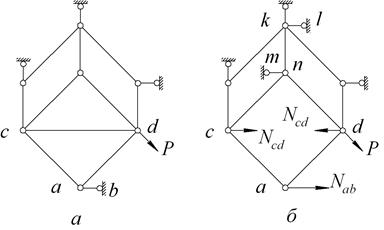
Иногда замены одного стержня оказывается недостаточно, чтобы получить заведомо неизменяемую преобразованную систему. В этих случаях можно осуществить замену двух или нескольких стержней.
|
| Рисунок 1.28 |
Стержневая система на рисунке 28,а может быть преобразована к простой неизменяемой заменой стержней  и
и 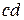 , например, на стержни
, например, на стержни 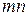 и
и 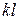 , в чём убеждаемся, используя метод разрушения. К узлам
, в чём убеждаемся, используя метод разрушения. К узлам 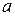 и
и  ,
, 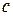 и
и 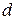 прикладываем в направлении устранённых стержней неизвестные усилия
прикладываем в направлении устранённых стержней неизвестные усилия 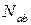 и
и 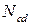 (рисунок 1.28,б). Систему уравнений для определения этих усилий запишем из условия равенства нулю полных усилий
(рисунок 1.28,б). Систему уравнений для определения этих усилий запишем из условия равенства нулю полных усилий 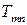 и
и 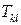 в заменяющих стержнях:
в заменяющих стержнях:
 (1.7)
(1.7)
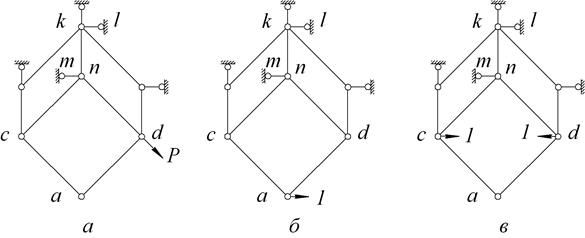
Здесь 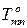 и
и 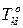 – усилия в заменяющих стержнях только от внешней нагрузки (рисунок 1.29,а);
– усилия в заменяющих стержнях только от внешней нагрузки (рисунок 1.29,а); 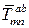 и
и 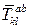 – усилия в заменяющих стержнях от единичных сил, приложенных к узлам
– усилия в заменяющих стержнях от единичных сил, приложенных к узлам 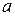 и
и  (рисунок 1.29,б);
(рисунок 1.29,б); 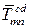 и
и 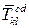 – усилия в заменяющих стержнях от единичных сил, приложенных к узлам
– усилия в заменяющих стержнях от единичных сил, приложенных к узлам 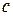 и
и 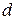 (рисунок 1.29,в).
(рисунок 1.29,в).
|
| Рисунок 1.29 |
Составим определитель из коэффициентов при неизвестных 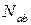 и
и 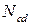 системы уравнений (1.7):
системы уравнений (1.7):
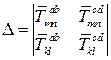 . (1.8)
. (1.8)
Если определитель 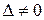 , то система уравнений (1.7) имеет решение. Исходная стержневая система статически определима и геометрически неизменяема.
, то система уравнений (1.7) имеет решение. Исходная стержневая система статически определима и геометрически неизменяема.
Если определитель 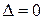 , то исходная система статически неопределима и геометрически изменяема.
, то исходная система статически неопределима и геометрически изменяема.
 2020-10-12
2020-10-12 250
250







