Цель занятия: усвоение понятий векторного и смешанного произведений векторов, выработка навыков вычисления векторного и смешанного произведений и использование их в приложениях.
Векторное произведение векторов
3.1.1 Определение. Векторным произведением неколлинеарных векторов 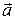 и
и  называется вектор, обозначаемый
называется вектор, обозначаемый  ×
×  , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям:
1) длина вектора  ×
×  равна
равна  , где
, где  ,
, 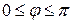 ;
;
2) вектор  ×
×  ортогонален обоим векторам
ортогонален обоим векторам  и
и  ;
;
3) тройка векторов  ,
,  ,
,  ×
×  является правой.
является правой.
Если векторы  и
и  коллинеарны, то полагают
коллинеарны, то полагают  ×
×  =
=  .
.
При вычислении векторного произведения полезно использовать его свойства. Перечислим их.
3.1.2  ×
×  = −
= −  ×
×  .
.
3.1.3  ×
×  =
=  ,
,  R.
R.
3.1.4  ×
× 
 ×
×  +
+  ×
×  .
.
3.1.5 Если  ×
×  =
=  , то векторы
, то векторы  ,
,  коллинеарны.
коллинеарны.
3.1.6 Длина  векторного произведения
векторного произведения 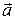 ×
×  равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах  и
и  как на сторонах.
как на сторонах.
Пусть векторы  и
и  заданы своими координатами относительно правого ортонормированного базиса
заданы своими координатами относительно правого ортонормированного базиса  , т.е.
, т.е. 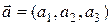 ,
,  . Тогда
. Тогда
 ×
×  =
=  . (9)
. (9)
Приложения векторного произведения в механике и физике связаны с понятием момента силы. Моментом силы  , приложенной к точке B, относительно некоторой точки А называется векторное произведение
, приложенной к точке B, относительно некоторой точки А называется векторное произведение  .
.
3.1.7 Пример. Заданы векторы  ,
,  . Найти координаты векторов
. Найти координаты векторов  ,
,  .
.
Решение. Вычисляем координаты вектора  по формуле (9):
по формуле (9):
 =
=  .
.
Координаты вектора  определим с помощью свойств векторного произведения векторов. Имеем
определим с помощью свойств векторного произведения векторов. Имеем  = =
= =  2
2 
 (поскольку
(поскольку  =0).
=0).
3.1.8 Пример. Найти площадь параллелограмма, построенного на векторах  , если
, если  ;
;  .
.
Решение. Имеем 
(поскольку  ). Итак
). Итак  (кв. ед.).
(кв. ед.).
 2020-10-12
2020-10-12 257
257








