2.2.1 Определение. Скалярным произведением векторов 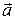 и
и 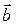 называется число, обозначаемое
называется число, обозначаемое 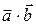 или
или 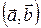 , равное
, равное 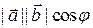 ,
, 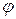 – угол между
– угол между 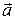 и
и  . Итак,
. Итак,
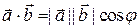 ,
, 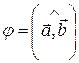 . (5)
. (5)
Основные свойства скалярного произведения:
1) 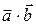 =
= 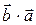 ; 3)
; 3) 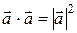 ; 5)
; 5) 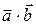 =0
=0  .
.
2)  =
=  =
= 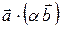 ; 4)
; 4) 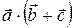 =
= 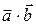 +
+  ;
;
Если векторы 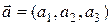 и
и 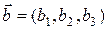 заданы в ортонормированном базисе
заданы в ортонормированном базисе 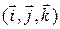 , то можно записать скалярное произведение
, то можно записать скалярное произведение 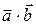 с помощью координат этих векторов:
с помощью координат этих векторов:
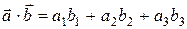 . (6)
. (6)
Угол между векторами:
 . (7)
. (7)
2.2.2 Определение. Проекцией вектора  на вектор
на вектор 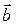 называется число
называется число
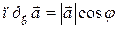 ,
,  (
(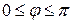 ). (8)
). (8)
С учетом (7) данную формулу можно записать в виде 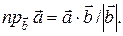
Числа
 ;
; 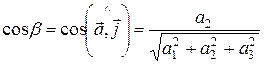 ;
; 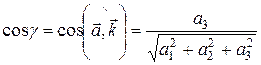 ;
;
называются направляющими косинусами вектора  .
.
Приложения скалярного произведения в механике и физике связаны с понятием работы постоянной силы. Если материальная точка, на которую действует сила 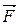 , переместилась из положения
, переместилась из положения  в положение
в положение  , то работаравна скалярному произведению
, то работаравна скалярному произведению  .
.
2.2.3 Пример. Найти скалярное произведение (3 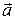 –2
–2 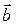 )×(5
)×(5 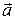 – 6
– 6  ), если
), если 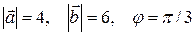 .
.
Решение. Согласно свойствам (1–4), (3  –2
–2 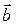 )×(5
)×(5 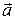 –6
–6 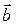 )=15
)=15 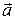 ×
× 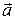
 ×
×  –
–
–10  ×
× 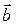 +12
+12 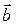 ×
× 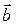 =15
=15 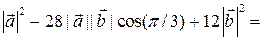
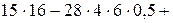
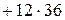 = 240 – 336 + 432 = 672 – 336 = 336.
= 240 – 336 + 432 = 672 – 336 = 336.
2.2.4 Пример. Найти угол между векторами  = (3, 4, 5),
= (3, 4, 5), 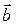 = (4, –5, 3).
= (4, –5, 3).
Решение. По формуле (7) получаем
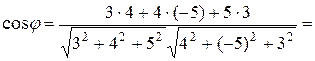
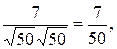

2.2.5 Пример. Доказать, что векторы  = (1,2,3),
= (1,2,3), 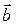 = (8, –1, –2) перпендикулярны.
= (8, –1, –2) перпендикулярны.
Решение. По формуле (6) находим: 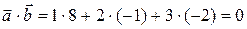 . Следовательно, по свойству (5) векторы
. Следовательно, по свойству (5) векторы  и
и 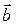 перпендикулярны.
перпендикулярны.
Упражнения
2.3.1 Найти координаты линейной комбинации 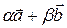 векторов
векторов 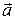 и
и  , если
, если
1)  ,
,  ,
,  ;
;
2)  ,
, 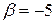 ,
,  .
.
2.3.2 Векторы  и
и 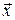 лежат в одной плоскости, известны их координаты в некотором базисе этой плоскости. Показать, что векторы
лежат в одной плоскости, известны их координаты в некотором базисе этой плоскости. Показать, что векторы  образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 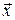 в этом базисе.
в этом базисе.
1) 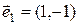 ,
, 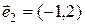 ,
, 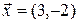 ;
;
2) 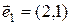 ,
, 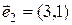 ,
, 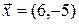 .
.
2.3.3 Даны векторы 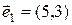 ,
,  ,
, 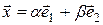 . Показать, что векторы
. Показать, что векторы  образуют базис на плоскости. Найти координаты вектора
образуют базис на плоскости. Найти координаты вектора 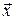 в «старом» базисе
в «старом» базисе 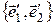 , если
, если
1) 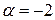 ,
,  ; 2)
; 2)  ,
,  .
.
2.3.4 Векторы 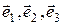 ,
,  заданы своими координатами в некотором базисе пространства. Показать, что векторы
заданы своими координатами в некотором базисе пространства. Показать, что векторы 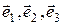 образуют базис пространства, и найти координаты вектора
образуют базис пространства, и найти координаты вектора  в базисе
в базисе  .
.
1) 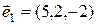 ,
, 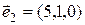 ,
, 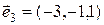 ,
,  ;
;
2) 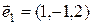 ,
,  ,
, 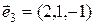 ,
, 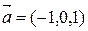 .
.
2.3.5 Вычислить 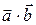 , если
, если 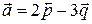 ,
, 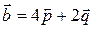 , где
, где  и
и  – единичные векторы, угол между которыми равен
– единичные векторы, угол между которыми равен 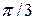 .
.
2.3.6 Даны точки 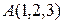 и
и 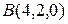 . Найти
. Найти  , направляющие косинусы вектора
, направляющие косинусы вектора 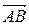 , величину проекции вектора
, величину проекции вектора 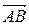 на базисный вектор
на базисный вектор  .
.
2.3.7 Найти неизвестную координату вектора 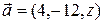 , если
, если  .
.
2.3.8 Найти угол между векторами 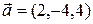 и
и 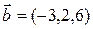 .
.
2.3.9 При каких 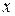 векторы
векторы 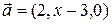 и
и 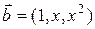 ортогональны?
ортогональны?
2.3.10 Даны вершины четырехугольника 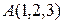 ,
, 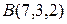 ,
,  ,
,  . Доказать, что его диагонали
. Доказать, что его диагонали  и
и 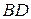 взаимно перпендикулярны.
взаимно перпендикулярны.
2.3.11 Найти 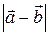 , если
, если  ,
,  ,
, 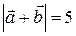 .
.
2.3.12 Доказать, что векторы 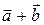 и
и  ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда 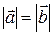 .
.
2.3.13 Даны три силы 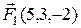 ,
,  и
и 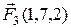 , приложенные в одной точке. Вычислить какую работу производит равнодействующая этих сил, когда точка приложения, двигаясь прямолинейно, перемещается из положения
, приложенные в одной точке. Вычислить какую работу производит равнодействующая этих сил, когда точка приложения, двигаясь прямолинейно, перемещается из положения 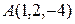 в положение
в положение  .
.
Контрольные задания
Рекомендуемая литература [1, гл. 1, §2–3], [2, гл. 2, §2.5, 2.6, 2.10–2.12], [3, гл. 1, §1.3, 1.4].
2.4.1 Доказать, что векторы  и
и 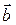 пространства равны тогда и только тогда, когда их координаты равны в любом базисе.
пространства равны тогда и только тогда, когда их координаты равны в любом базисе.
2.4.2 Векторы 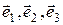 ,
, 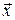 заданы в некотором базисе пространства. Показать, что векторы
заданы в некотором базисе пространства. Показать, что векторы 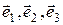 образуют базис пространства, и найти координаты вектора
образуют базис пространства, и найти координаты вектора 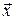 в базисе
в базисе  .
.
1) 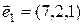 ,
, 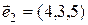 ,
,  ,
, 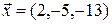 ;
;
2) 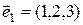 ,
, 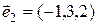 ,
, 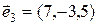 ,
,  .
.
2.4.3 Найти скалярное произведение векторов (–3 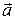 +4
+4 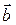 ) и (2
) и (2 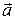 +3
+3  ), где
), где 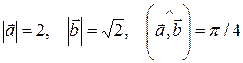 .
.
2.4.4 При каких 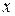 векторы
векторы  и
и 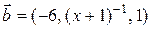 ортогональны?
ортогональны?
2.4.5 Найти вектор 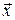 , коллинеарный вектору
, коллинеарный вектору 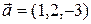 и удовлетворяющий равенству
и удовлетворяющий равенству 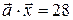 .
.
2.4.6 Даны векторы  и
и  . Найти проекцию вектора
. Найти проекцию вектора 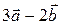 на вектор
на вектор 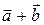 .
.
2.4.7 Вычислить работу силы 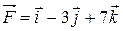 при перемещении материальной точки под действием этой силы из точки
при перемещении материальной точки под действием этой силы из точки  в точку
в точку 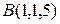 вдоль
вдоль 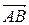 .
.
 2020-10-12
2020-10-12 200
200








