Смешанное произведение векторов

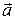3.2.1 Определение. Пусть , ,  –произвольные векторы. Возьмем векторное произведение × . Далее возьмем скалярное произведение ( × )  векторов ×  и . Полученное число называется смешанным произведением векторов , ,  (в указанном порядке) и обозначается ( × ) или .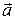

Перечислим основные свойства смешанного произведения.

3.2.2 Если векторы , ,  некомпланарны и образуют правую тройку, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах, как на ребрах, т.е.

( × ) = V.

Если же векторы , ,  некомпланарны и образуют левую тройку, то

( × ) =– V.

Векторы , ,  компланарны тогда и только тогда, когда

( × ) =0.

3.2.3 ( × ) =( × ) =( × ) .

Пусть , ,  заданы в ортонормированном базисе , , , . Тогда

                                 ( × ) =                                     (10)

Свойство (п.3.2.2) позволяет непосредственно или с помощью формулы (10) вычислять объемы некоторых тел. В частности, объем пирамиды с вершинами в точках , , ,  выражается следующим образом:

                        .                           (11)

Свойство (п.3.2.3) позволяет устанавливать, компланарны или некомпланарны векторы , , . Если векторы , ,  некомпланарны, то с помощью свойства (п.3.2.2) можно установить, какую тройку они образуют. А именно, если (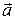 × ) >0, то тройка векторов , ,  правая, если же ( × ) <0, то тройка 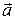, ,  левая.

3.2.4 Пример. Доказать, что точки А(5, 7, 2), B(3, 1, –1), C(9, 4, –4), D(1, 5, 0) лежат в одной плоскости.

Решение. Найдем координаты векторов: , . Найдем смешанное произведение полученных векторов:

,

Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.

3.2.5 Пример. Вычислить объем пирамиды, вершинами которой являются точки , , , .

Решение. Рассмотрим векторы (рисунок 5): , , .

У пирамиды, построенной на векторах 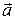, , ,та же высота, что и у параллелепипеда, а площадь основания в 2 раза меньше, поэтому

.

Заметим, что векторы , ,  образуют правую тройку, т.к. ( × ) >0. Объём пирамиды можно было найти прямо по формуле (11), однако, если нужно найти идругие параметры тела, удобнее начинать решение с построения векторов , , .

Упражнения

3.3.1 Даны векторы , , . Найти координаты следующих векторов:

1) × ; 2) ; 3) ×( ); 4) ( × ) .

3.3.2 Найти , если известны , , :

1) , , ; 2) , , .

3.3.3 Найти площадь параллелограмма, построенного на векторах ,  как на сторонах.

3.3.4 Найти площадь треугольника ABC, если:

1) , , ; 2) , , .

3.3.5 Найти длину высоты  треугольника ABC, если:

1) , , ; 2) , , .

3.3.6 Проверить; что векторы ,  коллинеарны, если векторы , , ,  связаны соотношениями × = × , × = × .

3.3.7 Упростить выражения:

1) ( + )× +( + )× +( + )× ;

2) ( + – )× –( + – )× +( + – )× .

3.3.8 Решить уравнение × = , где , .

3.3.9 Три силы , ,  приложены в точке . Определить момент равнодействующей этих сил относительно точки .

3.3.10 Векторы , ,  образуют правую тройку, взаимно перпендикулярны и , , . Вычислить ( × ) .

3.3.11 Пусть , ,  – произвольные векторы. Доказать, что:

1) (( + )×( + ))( – )=0;               2) (( – + )×( + )) =2 .

3.3.12 Найти объем параллелепипеда, построенного на векторах , , , как на сторонах. Установить, какую тройку образуют векторы , , .

3.3.13 Используя условие компланарности векторов, проверить, лежат ли следующие точки А, В, С, D в одной плоскости:

1) , , , ;

2) , , , .

3.3.14 Вычислить объем пирамиды, вершинами которой являются точки , , , .

3.3.15 В пирамиде с вершинами А, В, С, D найти длину высоты, проведенной из вершины D к грани ABС:

1) , , , ;

2) , , , .

Контрольные задания

Рекомендуемая литература [1, гл. 1, §3], [2, гл. 2, §2.13–2.17], [3, гл. 1, §1.13].

3.4.1 Показать, что четырехугольник АВСD есть параллелограмм, и найти его площадь, если , , , .

3.4.2 Определить площадь  с вершинами в точках , , .

3.4.3 Упростить выражение ( + + )×( + – ).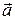

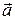3.4.4 Решить уравнение 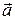× = , если известны ,  и первая координата вектора   равна 0.

3.4.5 Найти значение выражения , где  – правый ортонормированный базис.

3.4.6 Доказать, что точки , , ,  лежат в одной плоскости.

3.4.7 Вычислить объем пирамиды, вершинами которой являются точки , , , .

Прямая на плоскости

Цель занятия: усвоение способов задания прямой на плоскости, выработка навыков решения задач, связанных с прямыми на плоскости.