2.1.1 Определение. Два любых линейно независимых вектора 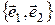 некоторой плоскости называются базисом этой плоскости. Три любых линейно независимых вектора
некоторой плоскости называются базисом этой плоскости. Три любых линейно независимых вектора 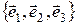 называют базисом пространства.
называют базисом пространства.
В пространстве нужно различать правые и левые базисы. Базис 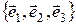 называется правым (левым), если при наблюдении с конца вектора
называется правым (левым), если при наблюдении с конца вектора  вращение вектора
вращение вектора 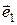 по кратчайшему пути к вектору
по кратчайшему пути к вектору  происходит против часовой стрелки (по часовой стрелке).
происходит против часовой стрелки (по часовой стрелке).
На рисунке 4,а изображен левый базис (вектор 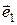 направлен от наблюдателя), а рисунке 4,б изображен правый базис (вектор
направлен от наблюдателя), а рисунке 4,б изображен правый базис (вектор  направлен от
направлен от 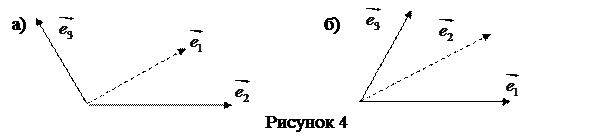 наблюдателя). Если векторы
наблюдателя). Если векторы 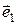 ,
,  ,
, 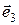 попарно ортогональны, то базис
попарно ортогональны, то базис 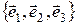 называется прямоугольным. Прямоугольный базис называется ортонормированным, если все векторы этого базиса имеют единичную длину. Обычно ортонормированный базис обозначается
называется прямоугольным. Прямоугольный базис называется ортонормированным, если все векторы этого базиса имеют единичную длину. Обычно ортонормированный базис обозначается  . Аналогично на плоскости. Если к базису на плоскости (в пространстве) добавить точку
. Аналогично на плоскости. Если к базису на плоскости (в пространстве) добавить точку  (начало отсчета), то возникает система координат на плоскости (в пространстве). Введенные для базисов понятия автоматически переносятся на системы координат.
(начало отсчета), то возникает система координат на плоскости (в пространстве). Введенные для базисов понятия автоматически переносятся на системы координат.
2.1.2 Теорема. Пусть 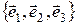 – произвольный базис в пространстве. Тогда для любого вектора
– произвольный базис в пространстве. Тогда для любого вектора 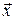 пространства имеет место разложение
пространства имеет место разложение
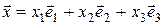 . (2)
. (2)
Разложение (2) единственно.
Аналогичное разложение имеет место для любого вектора некоторой плоскости  относительно любого базиса
относительно любого базиса  этой плоскости. Далее формулируем результаты для векторов в пространстве; соответствующие результаты для плоскости очевидны.
этой плоскости. Далее формулируем результаты для векторов в пространстве; соответствующие результаты для плоскости очевидны.
2.1.3 Определение. Коэффициенты 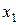 ,
,  ,
, 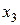 в разложении (2) называют координатами вектора
в разложении (2) называют координатами вектора 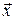 в базисе
в базисе 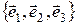 и пишут
и пишут 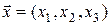 . Координатами точки M в системе координат
. Координатами точки M в системе координат  называют координаты вектора
называют координаты вектора 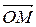 в базисе
в базисе 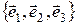 .
.
2.1.4 Теорема. Координаты вектора, являющегося линейной комбинацией других векторов, равны таким же линейным комбинациям соответствующих координат этих векторов.
Важным является вопрос о связи координат вектора в различных базисах. Пусть в пространстве заданы два базиса 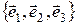 и
и  причем
причем
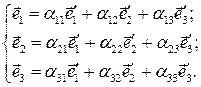 (3)
(3)
Если известны координаты 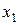 ,
,  ,
, 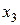 вектора
вектора 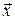 в «новом» базисе
в «новом» базисе  , то координаты
, то координаты  ,
, 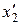 ,
,  этого вектора в «старом» базисе
этого вектора в «старом» базисе 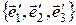 можно найти по формулам:
можно найти по формулам:
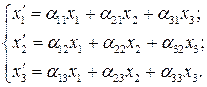 (4)
(4)
Более того, можно решить и обратную задачу. Если известны координаты 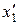 ,
, 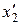 ,
,  вектора
вектора 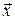 в базисе
в базисе 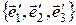 , то координаты
, то координаты 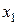 ,
,  ,
, 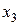 этого вектора
этого вектора 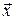 в «новом» базисе
в «новом» базисе 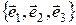 можно найти, решая систему линейных уравнений (4).
можно найти, решая систему линейных уравнений (4).
2.1.5 Пример. Даны векторы  ,
,  ,
, 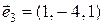 ,
, 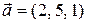 . Доказать, что векторы
. Доказать, что векторы 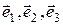 образуют базис в пространстве и найти координаты вектора
образуют базис в пространстве и найти координаты вектора 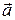 в этом базисе.
в этом базисе.
Решение. Убедимся, что векторы 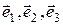 линейно независимы, т.е. векторное равенство
линейно независимы, т.е. векторное равенство 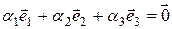 возможно лишь при
возможно лишь при  . Действительно, в соответствии с теоремой (п.2.1.4) имеем:
. Действительно, в соответствии с теоремой (п.2.1.4) имеем: 

Данная система имеет тривиальное решение ( ), если ее определитель
), если ее определитель
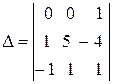
отличен от нуля. Убеждаемся, что  . Таким образом, тройка векторов
. Таким образом, тройка векторов 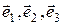 линейно независима и образует базис. Нам известны координаты вектора
линейно независима и образует базис. Нам известны координаты вектора 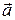 в некотором «старом» базисе
в некотором «старом» базисе  . Для того, чтобы найти координаты вектора
. Для того, чтобы найти координаты вектора 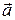 , в «новом» базисе
, в «новом» базисе 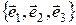 , составим систему уравнений вида (4) и решим её. В этой системе координаты векторов
, составим систему уравнений вида (4) и решим её. В этой системе координаты векторов 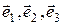 располагаются по столбцам:
располагаются по столбцам:
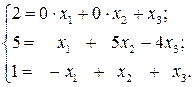
Вычисляем 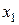 ,
, 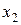 ,
, 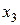 по формулам Крамера. Определитель данной системы уже найден:
по формулам Крамера. Определитель данной системы уже найден:  . Имеем далее
. Имеем далее
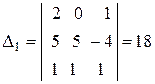 ;
;  ;
; 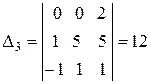 .
.
Отсюда 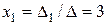 ,
,  ,
,  , т.е. в базисе
, т.е. в базисе 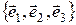 .
.
 2020-10-12
2020-10-12 283
283








