Считаем, что на плоскости задана ортонормированная система координат  . Координаты произвольной точки
. Координаты произвольной точки 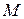 обозначаем
обозначаем  . Основополагающий результат о задании прямой на плоскости заключается в следующем.
. Основополагающий результат о задании прямой на плоскости заключается в следующем.
4.1.1 Теорема. Любая прямая на плоскости может быть задана уравнением вида
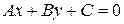 . (12)
. (12)
Наоборот, любое уравнение вида (12) задает на плоскости некоторую прямую.
Заметим, что вектор  ортогонален прямой (12) и называется нормальным. Уравнение (12) называют общим уравнением прямой. Различные модификации уравнения (12) связаны с различными способами задания прямых. Для успешного решения задач о прямых на плоскости необходимо усвоить следующие основные способы задания прямых.
ортогонален прямой (12) и называется нормальным. Уравнение (12) называют общим уравнением прямой. Различные модификации уравнения (12) связаны с различными способами задания прямых. Для успешного решения задач о прямых на плоскости необходимо усвоить следующие основные способы задания прямых.
4.1.2 Прямая  определяется одной своей точкой
определяется одной своей точкой 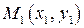 и нормальным вектором
и нормальным вектором  . Её уравнение имеет вид:
. Её уравнение имеет вид:
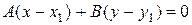 . (13)
. (13)
4.1.3 Прямая 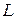 определяется двумя своими точками
определяется двумя своими точками  и
и 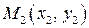 . Её уравнение имеет вид:
. Её уравнение имеет вид:
 или
или 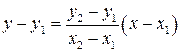 . (14)
. (14)
Число 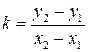 во втором выражении (14) называется угловым коэффициентом прямой
во втором выражении (14) называется угловым коэффициентом прямой 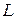 . Известно, что
. Известно, что  , где
, где  – угол между прямой
– угол между прямой 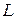 и осью
и осью 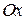 (или между
(или между 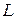 и вектором
и вектором 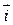 ).
).
4.1.4 Прямая 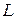 определяется одной своей точкой
определяется одной своей точкой 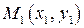 и угловым коэффициентом
и угловым коэффициентом 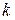 . Её уравнение имеет вид:
. Её уравнение имеет вид:
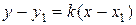 . (15)
. (15)
4.1.5 Прямая 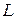 определяется одной своей точкой
определяется одной своей точкой 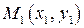 и вектором
и вектором 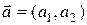 , параллельным
, параллельным 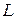 . Её уравнение имеет вид:
. Её уравнение имеет вид:
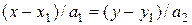 . (16)
. (16)
Вектор 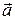 называется направляющим вектором прямой
называется направляющим вектором прямой 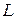 , а равенство (16) называют каноническим уравнением прямой L.
, а равенство (16) называют каноническим уравнением прямой L.
4.1.6 Если известна точка 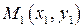 прямой
прямой  и еёнаправляющий вектор, то она может быть задана параметрическими уравнениями:
и еёнаправляющий вектор, то она может быть задана параметрическими уравнениями:
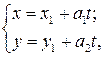 (17)
(17)
где  параметр,
параметр,  .
.
Пусть заданы две прямые  :
: 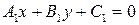 и
и 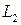 :
:  . Возможны следующие случаи взаимного расположения этих прямых:
. Возможны следующие случаи взаимного расположения этих прямых:
1) они совпадают, если  ;
;
2) они параллельны, если  ;
;
3) они пересекаются, если 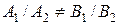 .
.
Угол между прямыми  и
и 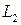 удобнее всего находить как угол между их направляющими векторами. Если же известны угловые коэффициенты
удобнее всего находить как угол между их направляющими векторами. Если же известны угловые коэффициенты  и
и 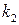 прямых
прямых  и
и 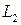 , то угол
, то угол 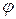 между ними можно найти поформуле
между ними можно найти поформуле
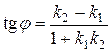 . (18)
. (18)
4.1.7 Пример. Даны две вершины 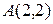 ,
,  треугольника
треугольника 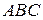 и точка
и точка  пересечения его высот (рисунок 6). Найти: уравнения сторон
пересечения его высот (рисунок 6). Найти: уравнения сторон 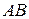 , СА и СВ, внутренний угол при вершине С, координаты точки С.
, СА и СВ, внутренний угол при вершине С, координаты точки С.
Решение.
 1 Воспользовавшись уравнением прямой, проходящей через две точки (см. формулу (13)), получим уравнение стороны
1 Воспользовавшись уравнением прямой, проходящей через две точки (см. формулу (13)), получим уравнение стороны 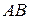 :
:
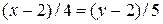 или
или  .
.
Далее, так как 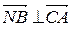 , а
, а 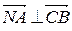 , то запишем уравнения сторон СА и СВ в виде (13), где
, то запишем уравнения сторон СА и СВ в виде (13), где  нормальный вектор к прямой, а
нормальный вектор к прямой, а 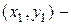 фиксированная точка на ней. Учитывая, что
фиксированная точка на ней. Учитывая, что  и
и  имеем
имеем
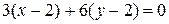 ,
, 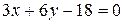 (
(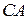 );
);
 ,
,  (
( ).
).
2 Угол 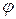 при вершине С есть угол между сторонами
при вершине С есть угол между сторонами 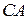 и
и  , который можно определить воспользовавшись выражением (18). Для этого запишем уравнения этих сторон в виде (15), т.е.:
, который можно определить воспользовавшись выражением (18). Для этого запишем уравнения этих сторон в виде (15), т.е.:
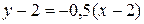 ;
;
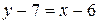 .
.
В этом случае согласно формуле (15) имеем  ,
, 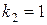 и в соответствии с (18) имеем
и в соответствии с (18) имеем 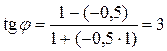 или
или  .
.
3 Для нахождения координат точки С составляем систему уравнений
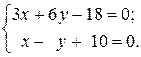
Решая ее, получаем 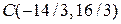 .
.
4.1.8 Пример. Задана прямая 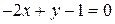 .Найти расстояние от точки
.Найти расстояние от точки  до данной прямой.
до данной прямой.
Решение. Прежде всего проверим принадлежит ли точка 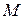 данной прямой
данной прямой  . Имеем
. Имеем 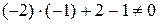 , значит
, значит  . Для нахождения расстояния от
. Для нахождения расстояния от 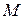 до
до  воспользуемся скалярным произведением векторов. На прямой
воспользуемся скалярным произведением векторов. На прямой  выберем произвольно точку
выберем произвольно точку  , например
, например 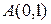 .Тогда расстояние от
.Тогда расстояние от 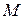 до
до  есть длина отрезка
есть длина отрезка 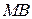 ,
, 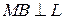 .
.
Длину отрезка  выразим с помощью скалярного произведения вектора
выразим с помощью скалярного произведения вектора 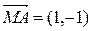 и нормального вектора
и нормального вектора 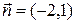 прямой
прямой  (рисунок 7). Имеем
(рисунок 7). Имеем
 , т.е.
, т.е. 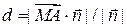 . (19)
. (19)
В соответствии с формулой (19) получаем
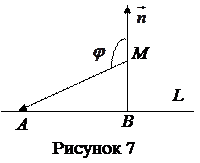
 .
.
Указанный способ нахождения расстояний применим и в случае плоскости, и в случае прямой в пространстве. В этом смысле он универсален, и мы рекомендуем применять его во всех аналогичных ситуациях.
Упражнения
4.2.1 Составить уравнение прямой, проходящей через точки 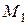 и
и 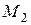 и сделать чертеж:
и сделать чертеж:
1)  ,
,  ; 2)
; 2) 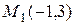 ,
, 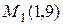 .
.
4.2.2 Составить параметрические уравнения прямой  .
.
4.2.3 Прямая задана параметрическими уравнениями 
Найти нормальный вектор этой прямой и записать общее уравнение этой прямой.
4.2.4 Дана прямая  . Составить уравнения прямых, проходящих через точку
. Составить уравнения прямых, проходящих через точку 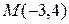 параллельно и перпендикулярно данной прямой.
параллельно и перпендикулярно данной прямой.
4.2.5 Известны вершины треугольника 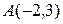 ,
,  ,
, 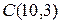 .
.
Требуется:
1) написать уравнения сторон этого треугольника;
2) написать уравнение высоты AD и найти её длину;
3) написать уравнение медианы BF и найти её длину;
4) найти угол при вершине A треугольника;
5) найти угол между высотой AD и медианой BF.
4.2.6 Вычислить расстояние от точки 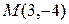 до прямой
до прямой 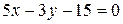 .
.
4.2.7 Написать уравнение прямой, проходящей посередине между параллельными прямыми 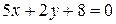 и
и 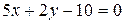 .
.
4.2.8 Написать уравнение прямой, параллельной прямой  и отстоящей от неё на расстоянии
и отстоящей от неё на расстоянии 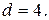
4.2.9 Записать уравнение прямой, проходящей через точку 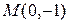 под углом
под углом  к прямой
к прямой 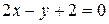 .
.
4.2.10 Известны уравнения одной из сторон ромба и одной из его диагоналей: 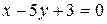 ,
, 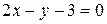 . Известна точка пересечения его диагоналей
. Известна точка пересечения его диагоналей 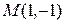 . Найти уравнения остальных сторон ромба.
. Найти уравнения остальных сторон ромба.
Контрольные задания
Рекомендуемая литература [1, гл. 2, §2–3], [2, гл. 5, §5.1–5.7].
4.3.1 Даны вершины треугольника 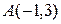 ,
, 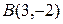 ,
, 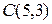 .
.
Требуется:
1) написать уравнения сторон этого треугольника;
2) написать уравнение высоты CD, проведённой из вершины C;
3) написать уравнение медианы BF, проведённой из вершины B;
4) найти угол при вершине A треугольника;
5) построить на чертеже  , высоту СD и медиану BF.
, высоту СD и медиану BF.
4.3.2 Вычислить расстояние от точки 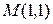 до прямой
до прямой  .
.
4.3.3 Известно уравнение одной из сторон параллелограмма  и уравнение двух его диагоналей
и уравнение двух его диагоналей  ,
,  . Найти уравнения остальных сторон параллелограмма.
. Найти уравнения остальных сторон параллелограмма.
 2020-10-12
2020-10-12 159
159








