Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть 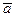 и
и 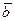 - два произвольных вектора. Возьмем произвольную точку О и построим вектор
- два произвольных вектора. Возьмем произвольную точку О и построим вектор  ; затем от точки А отложим вектор
; затем от точки А отложим вектор 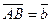 . Вектор
. Вектор 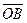 , соединяющий начало первого слагаемого вектора с концом второго называется суммой этих векторов
, соединяющий начало первого слагаемого вектора с концом второго называется суммой этих векторов 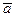 и
и 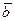 и обозначается
и обозначается 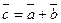 . (Рис. 1)
. (Рис. 1)
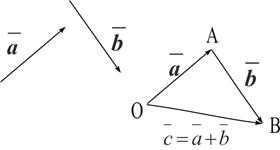
Рис. 1
Это правило сложения векторов называют правилом треугольника.
Сумму двух векторов можно построить также по правилу параллелограмма. Отложим от точки О векторы 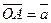 и
и 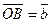 . Построим на этих векторах как на сторонах параллелограмм OACB. Вектор
. Построим на этих векторах как на сторонах параллелограмм OACB. Вектор 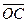 , служащий диагональю параллелограмма, проведенной из вершины О, является суммой векторов
, служащий диагональю параллелограмма, проведенной из вершины О, является суммой векторов 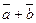 . (Рис. 2)
. (Рис. 2)
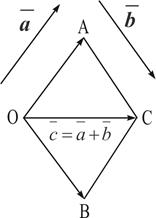
Рис. 2
Модуль вектора 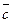 вычисляется по формуле
вычисляется по формуле
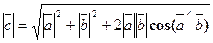
Разностью двух векторов 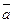 и
и  называется третий вектор
называется третий вектор 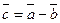 , сумма которого с вычитаемым вектором
, сумма которого с вычитаемым вектором  дает вектор
дает вектор 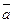 , т. е.
, т. е.  . (Рис. 3)
. (Рис. 3)
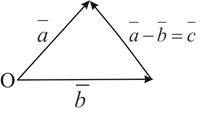
Если на векторах 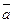 и
и  , отложенных из общей точки О, построить параллелограмм, то вектор
, отложенных из общей точки О, построить параллелограмм, то вектор 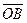 , совпадающий с одной диагональю параллелограмма, исходящей из точки О, равен сумме
, совпадающий с одной диагональю параллелограмма, исходящей из точки О, равен сумме 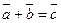 , а вектор
, а вектор  , совпадающий с другой диагональю равен разности
, совпадающий с другой диагональю равен разности 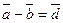 . (Рис. 4).
. (Рис. 4).
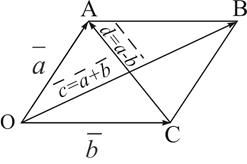
Рис. 4
Модуль вектора 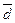 вычисляется по формуле
вычисляется по формуле 
При умножении вектора 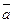 на скаляр (число) l получается вектор
на скаляр (число) l получается вектор  :
: 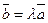 .
.
Полученный вектор  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1. 
2. вектор  коллинеарен вектору
коллинеарен вектору 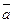
3. 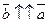 , если l > 0
, если l > 0
4. 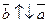 , если l < 0
, если l < 0
Замечание.
Т. к. вектор  коллинеарен вектору
коллинеарен вектору 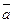 , то в дальнейшем условие коллинеарности векторов будем записывать в виде
, то в дальнейшем условие коллинеарности векторов будем записывать в виде 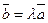 .
.
При умножении вектора 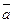 на скаляр (число) l получается вектор
на скаляр (число) l получается вектор  :
: 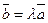
 2020-10-12
2020-10-12 159
159








