Определение: Три некомпланарных вектора 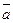 ,
, 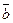 и
и 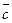 , приведенные к общему началу, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора
, приведенные к общему началу, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора 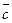 кратчайший поворот от первого вектора
кратчайший поворот от первого вектора 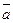 ко второму
ко второму 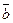 виден совершающимся против часовой стрелки (Рис. 1) и левую, если по часовой (Рис. 2).
виден совершающимся против часовой стрелки (Рис. 1) и левую, если по часовой (Рис. 2).
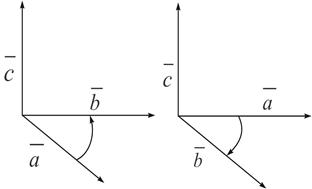 Рис. 1 Рис. 2
Рис. 1 Рис. 2
|
Определение: Векторным произведением вектора 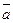 на вектор
на вектор 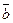 называется такой вектор
называется такой вектор 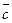 (Рис. 1), который
(Рис. 1), который
1. имеет длину, численно равную площади параллелограмма, построенного на векторах 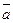 и
и 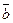 как на сторонах, т.е.
как на сторонах, т.е. 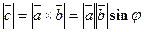 , где j - угол между векторами
, где j - угол между векторами 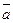 и
и 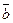 ;
;
2. перпендикулярен векторам 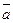 и
и 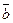 , т. е.
, т. е. 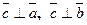 ;
;
3. направлен так, чтобы тройка векторов 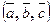 была правой.
была правой.
Векторное произведение обозначается  или
или  .
.
Следует запомнить, что в результате векторного произведения двух векторов получается вектор.
Свойства векторного произведения
- При перестановке множителей векторное произведение меняет направление на противоположное, сохраняя модуль
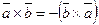 .
. - Сочетательное свойство по отношению к скалярному множителю
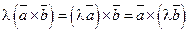 .
. - Распределительное свойство
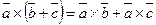 .
. - Два ненулевых вектора
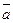 и
и 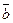 коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е.
коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. 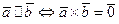 , если
, если 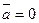 , либо
, либо  , либо
, либо 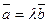 . В частности
. В частности 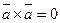 .
.
Выражение векторного произведения через координаты
Пусть заданы два вектора  и
и  . Найдем векторное произведение этих векторов, перемножая их как многочлены:
. Найдем векторное произведение этих векторов, перемножая их как многочлены:
 или
или 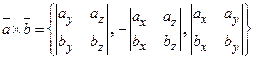 .
.
Полученную формулу можно записать еще короче  , так как правая часть предыдущего равенства соответствует разложению определителя третьего порядка по элементам первой строки.
, так как правая часть предыдущего равенства соответствует разложению определителя третьего порядка по элементам первой строки.
Приложения векторного произведения
Нахождение площади параллелограмма и треугольника.
Согласно определению векторного произведения векторов 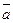 и
и 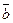 :
: 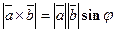 т. е. площадь параллелограмма
т. е. площадь параллелограмма  .
.
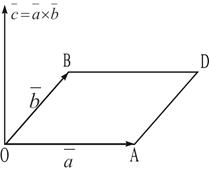
Рис. 3
Площадь треугольника - 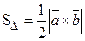 .
.
 2020-10-12
2020-10-12 170
170








