1. 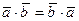 - переместительный закон
- переместительный закон
2. 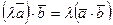 - сочетательный закон
- сочетательный закон
3. 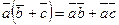 - распределительный закон
- распределительный закон
4. 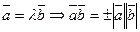
5. 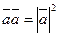 или
или 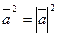
Если векторы коллинеарны, то  или
или  , а
, а 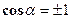 .
.
Скалярный квадрат вектора равен квадрату его модуля.
Определение: Скалярное произведение двух векторов, заданных своими координатами, равно сумме произведений одноименных координат этих векторов.
Пусть заданы два вектора 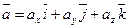 ,
, 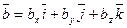 , тогда
, тогда
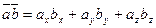
Замечание.
Если  , угол j - острый,
, угол j - острый,
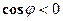 , угол j - тупой.
, угол j - тупой.
Приложения скалярного произведения
Угол между векторами: 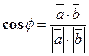 .
.
Угол между векторами в координатной форме: 
Определение: Векторы перпендикулярны тогда и только тогда, когда скалярное произведение этих векторов равно нулю: 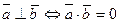 или
или 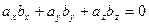
Нахождение проекции вектора 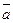 на направление, заданное вектором
на направление, заданное вектором 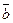 .
.
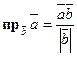 или
или
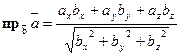
Проекция произвольного вектора  на какую – нибудь ось u определяется формулой
на какую – нибудь ось u определяется формулой 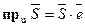 ,
, 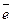 - единичный вектор, направленный по оси u.
- единичный вектор, направленный по оси u.
Замечание.
Если даны углы a, b, g, которые ось u составляет с координатными осями, то 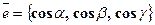 и для вычисления проекции вектора
и для вычисления проекции вектора 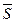 на ось u служит формула:
на ось u служит формула:
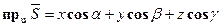
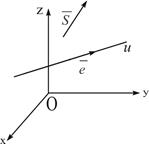
Рис. 2
Если вектор 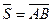 изображает перемещение материальной точки под действием постоянной силы
изображает перемещение материальной точки под действием постоянной силы 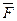 (Рис. 3), то работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.
(Рис. 3), то работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.
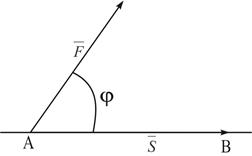
Рис. 3
Работа силы: 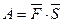 .
.
Задачи
Задача 1. Найти скалярное произведение векторов  и
и 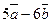 , если
, если  .
.
Решение: Имеем  (используем свойства скалярного произведения – формулы (5), (6), (7)). По формулам (2) и (9), получаем
(используем свойства скалярного произведения – формулы (5), (6), (7)). По формулам (2) и (9), получаем 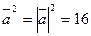 ,
, 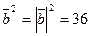 ,
, 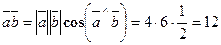
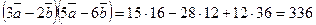
Задача 2. Даны точки  .
.
Вычислить 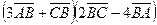 .
.
Решение: Найдем координаты векторов 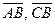 .
.
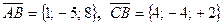 .
.
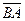 - противоположен вектору
- противоположен вектору  , следовательно,
, следовательно,  . Аналогично
. Аналогично  .
.
 ;
; 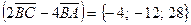 .
.
По формуле (10) найдем
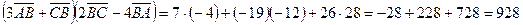 .
.
Задача 3. Вычислить угол, образованный векторами  и
и 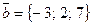 .
.
Решение: Используя формулу (11'), получаем
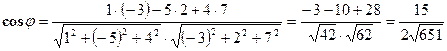
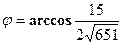
Задача 4. Даны векторы 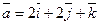 и
и 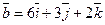 . Найти
. Найти  и
и 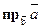 .
.
Решение: Используя формулу (13), получаем
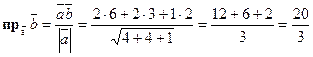

Задача 5. Дан вектор 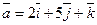 . Найти его проекцию на ось u, составляющую с координатными осями равные острые углы.
. Найти его проекцию на ось u, составляющую с координатными осями равные острые углы.
Решение: Т. к. ось u составляет с координатными осями равные острые углы, т. е. 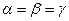 , то
, то 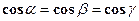 .
.
Но  , и т. к. в этой сумме все слагаемые между собой равны, то
, и т. к. в этой сумме все слагаемые между собой равны, то 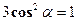 ;
;  ;
;  , тогда
, тогда 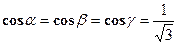 (знак плюс перед корнем взят потому, что по условию углы a, b, g - острые, значит косинусы их положительны). Т. к. по условию
(знак плюс перед корнем взят потому, что по условию углы a, b, g - острые, значит косинусы их положительны). Т. к. по условию  ,
, 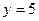 ,
, 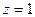 , то по формуле получаем
, то по формуле получаем 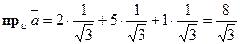 .
.
Лекция №8. Векторное произведение двух векторов. Смешанное произведение трех векторов.
 2020-10-12
2020-10-12 114
114








