2020-10-12
102
Пусть точка А твердого тела неподвижно закреплена, а в точке B (Рис. 4) приложена сила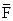 
. При этом возникает вращающий момент, численно равный 
- площади параллелограмма, построенного на векторах 
и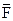 
.
Рис. 4
Вектор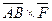 
- представляет собой момент силы 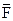относительно точки А.
Задачи
Задача 1. Раскрыть скобки и упростить выражение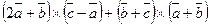 
.
Решение: Используя свойства векторного произведения (формулы 4, 5), получаем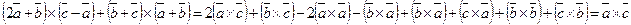 
,
т. к.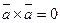 
, 
, 
, 
.
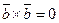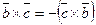Задача 2. Найти площадь параллелограмма, построенного на векторах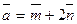 
и 
, где 
- единичные векторы, образующие угол 
.
Решение: 
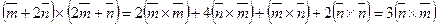, т. к. 
, 
, 
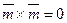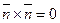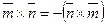
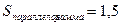
Задача 3. Найти векторное произведение векторов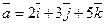 
и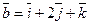 
.
Решение: По формуле (7) имеем
Задача 4. Найти площадь треугольника, координаты вершин которого известны: 
, 
, 
.
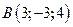Решение:
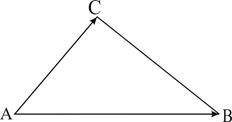Рассмотрим векторы и 
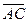. Площадь треугольника ABC есть половина площади параллелограмма, построенного на векторах и .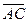
, 
.
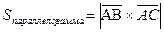Найдем проекции векторов и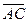 
на координатные оси:
, 
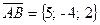По формулам (7) для векторного произведения векторов найдем, что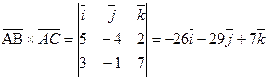 
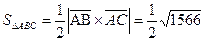
Смешанное произведение трех векторов.
|
|
|
Определение: Смешанным произведением трех векторов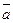 
, 
, 
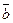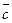называется число, равное векторному произведению 
, умноженному скалярно на вектор .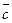
Обозначение смешанного произведения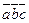 
В результате смешанного произведения трех векторов получается число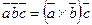 
.
Если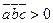 
, то тройка векторов 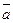, , 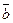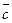- правая.
Если 
, то тройка векторов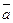 
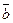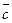, , - левая.
Определение: Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю, т. е.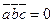 
Û векторы 
, 
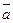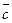, - компланарны.
