Система векторов а1, а2,...ап, называется линейно зависимой, если существуют такие числа α1, α2, … αп, одновременно не равные нулю,
что линейная комбинация этих векторов с этими коэффициентами равна нулевому вектору, т.е. α1 а1 + α2 а2 + … + αп ап = 0.
Система векторов а1, а2,...ап, называется линейно независимой, если, линейная комбинация этих векторов равна нулевому вектору α1 а1 + α2 а2 + …
+ αп ап = 0 только в одном случае, когда все коэффициенты α1, α2,… αп, одновременно равные нулю.
Системы линейно зависимых и линейно независимых векторов обладают следующими свойствами:
1о) Система векторов а1, а2,...ап ( п 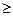 2) линейно зависима тогда и только тогда, когда хотя бы один вектор этой системы является линейной комбинации остальных векторов.
2) линейно зависима тогда и только тогда, когда хотя бы один вектор этой системы является линейной комбинации остальных векторов.
2о) Если система содержит нулевой вектор, то она линейно зависима.
3о) Если подсистема данной системы векторов линейно зависима, то и вся система векторов линейно зависима.
4о) Если система векторов линейно независима, то и любая её подсистема линейно независима.
Теорема о коллинеарных векторах.
Если векторы а и b коллинеарны и вектор а ненулевой вектор, то существует единственное число λ такое, что а = λ b.
Теорема о компланарных векторах.
Если векторы а, b и с компланарны и векторы а и b не коллинеарны, то существует единственная пара чисел λ и β такие, что с = λ а + β b.
Теоремы о линейной зависимости системы двух и трех векторов:
1. Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда эти векторы коллинеарны.
2. Система, состоящая их трех векторов, линейно зависима тогда и только тогда, когда эти векторы компланарны.
1.17. Система, состоящая из векторов а и b линейно зависима. Всегда ли существует такое число х, что а = х b? Если нет, то привести пример.
ОТВЕТ.. Нет, если а 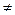 0, b = 0.
0, b = 0.
1.18. Система, состоящая из векторов а, b и с линейно зависима. Всегда ли существует такие числа х и у, что с = х а + у b? Если нет, то привести пример.
ОТВЕТ.. Нет, если векторы а и b коллинеарны, а векторы а и с не коллинеарны.
1.19. Для каких векторов а и b каждый вектор можно выразить через другой.
ОТВЕТ.. Если а 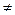 0 и b
0 и b 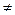 0 или а = b = 0
0 или а = b = 0
1.20. Для каких векторов а, b, с каждый вектор можно выразить через два других.
ОТВЕТ. Если векторы а, b, с компланарны и попарно не коллинеарны или а = b = с = 0.
ПРИМЕР 1. 6
Векторы а, b, с не компланарны. Выяснить, является ли следующая система векторов линейно зависимой: а) { а + 3 b, 2 а – с, 4 а + 6 b – с },
б) { а + b, b + с, с + а}.
РЕШЕНИЕ
Для того, чтобы выяснить, является ли данная система векторов линейно зависимой надо, исходя из определения линейно зависимой системы векторов, найти такие числа х, у, z, одновременно не равные нулю, что линейная комбинация данных вектор с коэффициентами х, у, z будет равна нулевому вектору. Если же таких чисел, одновременно не равных нулю, не найдется, то данная система векторов будет линейно независимой.
а) Приравняем линейную комбинацию векторов данной системы к нулевому вектору
х(а + 3 b) + у ( 2 а – с) + z (4 а + 6 b – с) = 0 (1)
Теперь исходя из свойств сложения векторов и свойств произведения векторов на число, раскроем скобки и найдем коэффициенты при векторах а, b и с.
Из (1) следует: х а + 3х b + 2у а – у с + 4z а + 6z b – z с = 0 и
(х + 2у + 4 z) а + (3х + 6 z) b + (-у – z) с = 0 (2)
Так как векторы а, в, с не компланарны, то система векторов { а, b, с} линейно независима, тогда из определения линейно независимой системы векторов следует что равенство (2) выполнятся только тогда, когда все три коэффициента при векторах а, b, с одновременно равны нулю, следовательно,
х + 2у + 4 z =0, 3х + 6 z = 0, -у – z = 0.
Выражая из второго и третьего из этих уравнений х и у через z, получим,
х = -2z, у = - z.
Подставляя эти выражения для х и у в первое уравнение получим:
-2z + 2(-z) + 4 z = 0. Это равенство верно для любых значений z, следовательно, решением трех полученных уравнений являются любые числа х, у, z, удовлетворяющие условиям х = -2 z, у = - z. В частности, если
z = 1, то х = -2, у = -1.
Таким образом, мы нашли ненулевые коэффициенты х = - 2, у = - 1. z = 1, для который верно равенство (2), а значит и равенство (1). Следовательно, данная система векторов линейно зависима.
б) Приравняем линейную комбинацию векторов данной системы к нулевому вектору
х(а + b) + у(b + с) + z(с + а) = 0 (3)
Из (3) следует:
(х + z) а + (х + у) b + (у + z) с = 0 (4)
Так как векторы а, b, с не компланарны, то система векторов { а, b, с } линейно независима, тогда из определения линейно независимой системы векторов следует что равенство (4) верно только в одном случае, когда все коэффициенты при векторах а, b, с равны нулю.
х + z = 0, х + у = 0, у + z = 0.
Выражая из второго и третьего из этих уравнений х и z через у, получим,
х = - у, z = -у.
Подставляя эти выражения для х и z в первое уравнение получим:
-у - у = 0. и значит у = 0, поэтому х = 0 и z = 0
Таким образом, мы выяснили, что равенство (4), а значит и равенство (3) верны только в том случае, когда х = у = z = 0. Следовательно, данная система векторов линейно независима. ■
1.21. Векторы а и b не коллинеарные. Выяснить, являются ли данные системы векторов линейно независимыми: а) {2 а, - 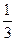 b}, б) {
b}, б) { 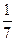 а – b, -4 b, а + b},
а – b, -4 b, а + b},
в) {-3 а, 5 b, а}, г) {2 а, 0, 3 b}.
ОТВЕТ. а) линейно независимы, б), в) - линейно зависимы.
1.22. Векторы а, b, с не компланарны. Являются ли следующие системы векторов линейно зависимыми: а) { а + b, а - b, а}, б) (4 а, -6 b, 3 с},
в) { а, а + b, с}, г) (3 а + b, а + с, b -2 с}?
ОТВЕТ. а) линейно зависимы, б), в), г) - линейно независимы.
1.23. Векторы а, b, с не компланарны. Выяснить, при каких значениях х векторы (а + b), (b + с), (х а + с) также не компланарны.
ОТВЕТ.. х 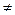 – 1.
– 1.
Координаты вектора в данном базисе.
Базисом векторного пространства называется такая упорядоченная линейно независимая система векторов, что любой вектор пространства можно представить в виде линейной комбинации векторов этой системы.
В трехмерном векторном пространстве базис состоит из трех векторов, который обычно обозначается так: { е1, е2, е3 }.
Базис называется ортонормированным, если длины всех базисных векторов равны единицы, и базисные векторы попарно перпендикулярны. Ортонормированный базис обычно обозначается так: { i, j, k }.
Координатами вектора m в базисе { е1, е2, е3 } называются коэффициенты разложения вектора m по векторам базиса, т.е. если m = х е1 + у е2 + z е3, то числа х, у, z - координаты вектора m. В этом случае будем записывать m (х, у, z).
Имеет место теорема о координатах линейной комбинации:
если вектор m = x а + y b и а (а 1 ,а 2 ,а 3 ), b ( b1,b2,b3 ) m ( m1,m2,m3 ), то
m1 =x a 1 + y b1, m2 =x a 2 + y b2, m3 =x a 3 + y b3.
1.24. Даны векторы а (2, 3, -1), b (0,1,4), с (1,0,-3). Найти координаты векторов: а) 2 а - b -2 с, б) а - b -3 с, в) а + 2 b + 3 с), г) а - b – с,
д) 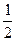 (а + b), е)
(а + b), е) 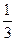 (а - 2 b + с).
(а - 2 b + с).
ОТВЕТ. а) (2,5,0), б) (-1,2,4), в) (5,5,-2), г) (1,2,-2), д) (1,1,3), е) (1, 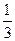 ,-4)
,-4)
ПРИМЕР 1.7
Даны векторы а (1,1,2), b ( -2, 3 5), с (-4,1,1), d (0, -1, 3) Можно ли вектор d представить в виде линейной комбинации векторов а, b, с? Если да, то найти коэффициенты этой линейной комбинации.
РЕШЕНИЕ
Выясним, существуют ли такие числи х, у, z, что
d = х а + у b + z с. (1)
По теореме о координатах линейной комбинации векторов из равенства (1) получаем выражение для первой координаты вектора d через первые координаты векторов а, b, с, и аналогичные выражения для вторых и третьих координат
0 = х - 2у - 4 z (2)
-1 = х + 3у + z (3)
3 = 2х + 5у + z (4)
Выясним, имеет ли эта система решение. Из (2) следует, что
х = 2у + 4z (5)
Затем, подставляя (5) в (3) и (4), получаем:
5у + 5z = -1 (6)
9у + 9z = 3 (7)
Система, состоящая из уравнений (2), (3), (4), равносильна системе, состоящей из уравнений (5), (6), (7). Ясно, что последняя система не имеет решений, следовательно, и данная система не имеет решений,. Поэтому вектор d нельзяпредставить в виде линейной комбинации векторов а, b, с. ■
1.25. Определить, какие из данных троек векторов линейно зависимы:
а) а (-3,0, 2), b (2, 1, -4), с (11, -2, -2); б) а (1, 0, 7), b (-1, 2, 4), с (3, 2, 1);
в) а (5, -1,4), b (3,-5, 2), с (-1,-13, -2).
ОТВЕТ.. а), с) линейно зависимы.
1.26. Представить вектор d как линейную комбинацию векторов а, b, с:
1) а (2,3,1), b ( 5, 7, 0), с (3, -2, 4), d (4, 12, -3);
2) а (5, -2, 0), b ( 0, -3, 4), с (-6, 0, 1), d (25, -22, 16);
3) а (3, 5, 6), b ( 2, -7, 1), с (12, 0, 6), d (0, 20, 18).
ОТВЕТ. 1) d = а + b + с, 2) d = 5 а + 4 b, 3) d = 4 а – с.
1.27. Можно ли вектор d (1,1,1) представить в виде линейной комбинации векторов а (1,-1,0), b ( 2,2,1), с (0,-4,-1)?
ОТВЕТ.. Нет.
1.28. Даны векторы а (х, 3, 4), b ( -1, 5, у). Существуют ли такие числа х и у, для которых система векторов { а, b } линейно зависима?
ОТВЕТ. Да, х = -  , у =
, у = 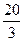 .
.
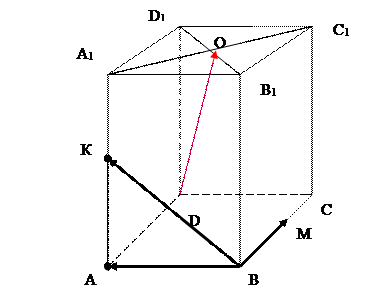
ПРИМЕР 1.8
В параллелепипеде АВСDА1В1С1D1 К – середина ребра АА1, точка М лежит на ребре ВС и ВМ = 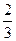 ВС, О = А1С1
ВС, О = А1С1 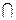 В1D1. Найти координаты вектора
В1D1. Найти координаты вектора 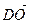 в базисе {
в базисе { 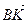 ,
, 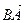 ,
, 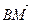 }.
}.
РЕШЕНИЕ
Так как координаты вектора в данном базисе это коэффициенты разложения этого вектора по векторам базиса, то данную задачу можно сформулировать так: выразить вектор 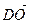 через векторы
через векторы 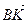 ,
, 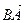 ,
, 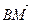 , поэтому будем действовать так же, как при решении ПРИМЕРА 1.3.
, поэтому будем действовать так же, как при решении ПРИМЕРА 1.3.
1) 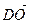 =
= 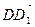 +
+ 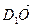 =
= 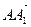 +
+ 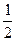
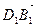 = 2
= 2 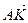 +
+ 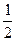
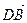 , т.е.
, т.е.
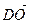 = 2
= 2 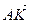 +
+ 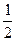
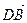 . (1).
. (1).
2) Выразим вектор 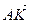 через базисные векторы.
через базисные векторы.
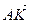 =
= 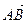 +
+ 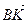 = -
= - 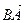 +
+ 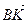 . (2)
. (2)
3) Выразим вектор 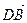 через базисные векторы.
через базисные векторы.
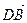 =
= 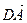 +
+ 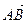 =
= 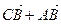 = -
= - 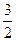
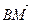 –
– 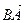 (3)
(3)
4) Подставим (2) и (3) в (1), получим
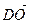 = 2(-
= 2(- 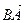 +
+ 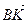 ) +
) + 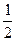 (-
(- 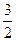
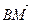 –
– 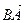 ) = 2
) = 2 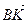 –
– 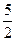
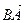 –
– 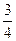
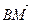 .
.
Следовательно, первая координата вектора 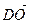 равна 2, вторая координата равна -
равна 2, вторая координата равна - 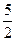 , третья координата равна -
, третья координата равна - 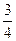 , т.е.
, т.е. 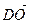 (2, -
(2, - 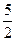 , -
, - 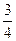 ).
).
ОТВЕТ. 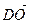 (2, -
(2, - 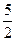 , -
, - 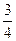 ).
).
1.29. АВСD – тетраэдр. М и К – точки пересечения медиан граней ВСD и АDС, N – середина АВ, Р 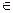 ВС и ВР: РС = 1: 2. Найти координаты векторов
ВС и ВР: РС = 1: 2. Найти координаты векторов 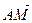 ,
, 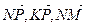 в базисе {
в базисе { 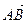 ,
, 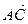 ,
, 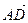 }.
}.
ОТВЕТ. 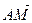 (
( 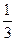 ,
, 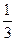 ,
, 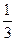 ),
), 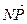 (
(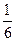 ,
, 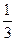 , 0),
, 0), 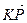 (
(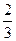 ,0, -
,0, - 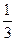 ),
), 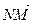 (-
(- 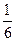 ,
, 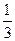 ,
, 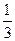 ).
).
1.30. АВСD – тетраэдр. N и К середины ребер ВС и АС. Найти координаты векторов 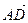 и
и 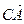 в базисе {
в базисе { 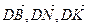 }.
}.
ОТВЕТ. 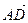 (-1,2,-2),
(-1,2,-2), 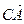 (2,-4,2).
(2,-4,2).
1.31. В тетраэдре АВСD М- середина ВС, а N – точка пересечения медиан грани АDС. Найти координаты векторов 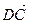 и
и 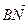 в базисе {
в базисе { 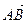 ,
, 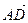 ,
, 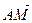 }.
}.
ОТВЕТ. 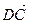 (-1,-1,2),
(-1,-1,2), 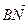 (-
(- 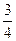 ,
, 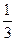 ,
, 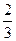 ).
).
1.32. В тетраэдре АВСD N - середина ВС, а М и К – точки пересечения медиан граней ВСD и АВD. Найти координаты векторов 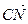 и
и 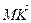 в базисе {
в базисе { 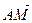 ,
, 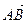 ,
, 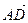 }.
}.
ОТВЕТ. 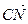 (-
(- 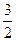 , 1,
, 1, 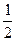 ),
), 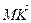 (-1,
(-1, 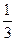 ,
, 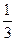 ).
).
 2020-10-12
2020-10-12 849
849








