Скалярное произведение векторов

           Скалярным произведением векторов а и b называется число, равное произведения длин этих векторов и косинуса угла между ними

     а b = │ а ││ b │cos (а b ).

          Скалярное произведение векторов обладает следующими свойствами: для любых векторов а, b, c и любого числа λ

     1) а b = b a, 2) (a + b) c = a c + b c, 3) (λ a) b = a (λ b) = λ (a b).

        Если известны координаты векторов а и b в ортонормированном базисе { i, j, k } а (а ₁ ,а ₂ ,а ₃ ), b (b ₁ ,b ₂ ,b ₃ ), то имеют место формулы

                                                                        

        a b = а ₁ b ₁ + а ₂ b ₂ + а ₃ b ₃ ,      │ а │=

                          cos (а, b ) =    

1.33. АВСD – ромб с углом А равным 60° и стороной АВ равной 4. Найти скалярное произведение .

ОТВЕТ.. 8.

1.34. М – точка пересечения медиан равностороннего треугольника АВС со стороной равной 2. Найти скалярное произведение .

ОТВЕТ.. - .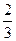

 

1.35. АВСD – квадрат стороной равной 5. Найти скалярное произведение .

ОТВЕТ. -25.

 

         ЗАМЕЧАНИЕ Во всех задачах этого пункта будем считать, что дан ортонормированный базис

 

1.36. а (1,-1,3), b ( 2,4,-5), с (1,-2,1). Найти: 1) а b, 2) | с |, 3) Соs (b, с).

       4) (а + b + 5 с) · ( 2 b - 4 с), 5) (а – b) · (с – а).

ОТВЕТ. 1) -17, 2) , 3) - , 4) -164, 5) -11.

      ПРИМЕР 1.11

               Дан треугольник АВС и ортонормированный базис. М  ВС и ВМ: МС = ,

      Р АС и АР: РС = 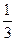. АМ 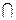ВР = АD. Найти Соs МDР, если 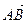(0,9,12), 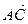(12,24,36).

 

     РЕШЕНИЕ  

Угол МDР равен углу между векторами  и  или углу между сонаправленными с ними векторами  и  Поэтому Соs МDР = Соs (, ) =

     Найдем координаты векторов   и .  =  =   + .

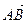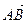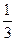
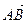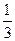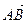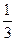
Поэтому  (3, -3, -3)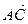.  =  +  =  +  =  + (  + ) =          + . Поэтому  (4, 14,20).

Соs (, ) = (12 - 52 – 60):  = - .

ОТВЕТ. Соs МDР = - .

  

1.36. В параллелограмме АВСD 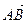(-8,0,6), 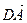(-3,-4,0). Найти ВАD.

 ОТВЕТ.. – .

 

1.37. Дан базис{ i, j, k }.Найти косинусы углов, образованных вектором

а (5, - , 3) с базисными векторами i, j, k.

ОТВЕТ. cоs (i, а) = ,  cоs (j, а) = - , cоs (k,а) = .

 

1.38. Дан тетраэдр АВСD. 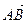(1,4,1), (2,-3,-2),  (0,5,0). Найти Соs ВАМ, где М – середина СD.

ОТВЕТ. ,

 

1.39. В пространственном четырехугольнике АВСD 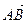(1,6,-2),

 (5,3,-1), (1,-7,-1). Доказать, что диагонали четырехугольника перпендикуляры.

 

1.40. Дан четырехугольник АВСD. 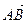(6,0,-8), (0,10,0), (-6,0,8). Доказать, что этот четырехугольник является квадратом.

1.41. Найти длину медианы АМ треугольника АВС и угол АМВ, если 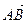(1,-1,2), (3,5,-4).

ОТВЕТ.. АМ = 3, cоs АМВ ,

1.42. Найти длины медианы АD треугольника АВС, если 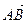 (0,4,0),

 (-3, 0,0).

ОТВЕТ. АD = .

 

1.43. В треугольнике АВС 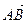 (2,1,3),  (0,1,1) Найти косинус угла между медианой АМ и высотой АН.

ОТВЕТ. cоs МАН = .

 

1.44. АМ и АD медиана и биссектриса треугольника АВС. Найти косинус угла МАD, если 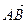 (0,4,0),  (-3, 0,0).

ОТВЕТ. cоs МАD = .

 

1.45. В треугольнике АВС АМ - медиана, АD –биссектриса, АН – высота. Найти длину АМ и косинус угла НАD, если 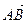 (2,0,0),  (0,0,4). 

ОТВЕТ.. АМ = , Соs НАD = .