Представление игры с природой в виде S-игры

Статистические игры без эксперимента.

Статистические игры могут быть представлены в виде S-игры, как это делалось в стратегических играх, т. к. и в данном случае представление в виде S-игры ориентировано на минимаксное решение.

Рассмотрим представление на примере.

Пример: задача о замене оборудования. Дорогое оборудование после k лет эксплуатации может оказаться в одном из трёх состояний.

1. z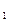=V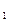— оборудование работоспособно, требует лишь мелкого ремонта;

2. z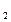=V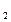— некоторые детали серьёзно износились, требуется капитальный ремонт;

3. z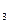=V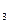— основные детали очень износились, требуется полная замена.

Прошлый годы эксплуатации показывают, что оборудование может находиться в 1-ом состоянии с вероятностью q = 0,2; во 2-ом состоянии — с вероятностью q = 0,5; в 3-ем состоянии — с вероятностью q = 0,3. В качестве статистика рассмотрим руководство предприятия, которое может принять 3 различных способа действий:

1. x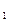=a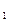— оставить оборудование работать ещё год, сделав мелкий ремонт своими силами;

2. x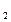=a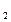— будет вызвана организация для выполнения капитального ремонта;

3. x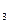= a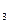— будет демонтировано старое и куплено новое оборудование.

В примере установлена матрица потерь, которые понесёт предприниматель, принимая решение x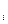= a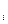в условиях z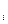=V.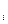

Таблица потерь:

V	q(V)	a1	a2	a3	L(V,a1)	L(V,a2)	L(V,a3)
V1	0,2				4,8	3,4	3,9
V2	0,5
V3	0,3

Очевидно, что наименьшие потери предприятие понесёт при стратегии a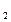(x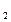). Т. о. определяющую средние потери a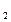(x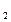) называют байесовской потерей.

В пространстве эту игру можно представить следующим образом:

C1 = (1,5,7)

C2 = (3,2,6)

C3 = (5,4,3)

Статистик минимизирует свои потери, играя за природу.

Пример:

На обработку поступает сырьё.

Вероятность

0,6 V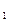<ПДК (предельно допустимая концентрация)

0,4 V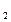>ПДК

Для обработки этого сырья можно использовать три технологии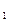 a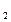, a, a. Убытки, которые понесёт предприятие, представлены в следующей таблице:

V	q(V)	a1	a2	a3	L(V,a1)	L(V,a2)	L(V,a3)
V1	0,6					1,8	1,8+0,8=2,6
V2	0,4

а — оптимальная байесовская стратегия. Эту игру можно рассмотреть в виде S-игры на плоскости:

S* — линейно выпуклая оболочка игры

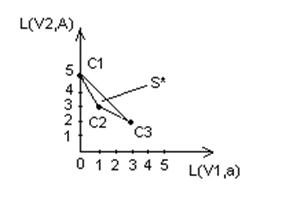
Эта линейная выпуклая оболочка представляет область всех возможных стратегий статистика, как чистых, так и смешанных. Возникает вопрос: как выбирать оптимальную стратегию в этой игре?

Вопрос о выборе оптимальной стратегии остаётся открытым. Тем не менее, не давая ответа на вопрос что нужно делать, можно ответить на вопрос, что делать не нужно в этой игре.

Вводится понятие допустимых стратегий, аналогичное понятию недоминируемых стратегий в матричных играх).