Эксперимента

Анализ целесообразности проведения

Пусть в результате проведения единичного эксперимента может появиться k исходов: 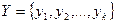. Предположим, что имеются вероятности 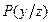. Множество состояний природы: 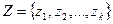. Обозначим 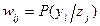— вероятность появления исхода эксперимента 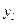при состоянии природы .

.

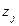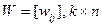Ясно, что для каждого j: .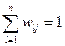

Считаем, что матрица W известна статистику. Кроме этого известна матрица выигрышей 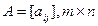, которая получена статистиком, используя стратегию 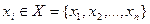в состоянии природы .

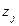Статистику известна стоимость проведения единичного эксперимента – с.

Анализируя эту информацию, статистик должен дать ответы на два вопроса:

1. целесообразно или нет проведение эксперимента.

2. какую из решающих функций необходимо при этом использовать, если эксперимент будет проводиться.

Рассмотрим обоснования для оценки ответа на первый вопрос.

Пусть в результате эксперимента произошел некоторый исход 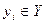. Апостериорные вероятности состояния природы 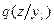обозначим в виде 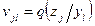. Эти вероятности определяют некоторую матрицу 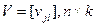, которую можно определить через апостериорные вероятности 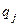по формуле Байеса:

.

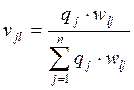С помощью апостериорных вероятностей для каждой из чистых стратегий статистика 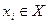можно определить условно средний выигрыш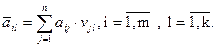

Оптимальную стратегию .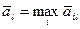

Величины являются случайными величинами, вероятность их появления совпадает с вероятностью исхода эксперимента.

Обозначим через 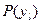вероятность l-ого исхода эксперимента. Она будет определяться вероятностью исхода при всех состояниях природы:

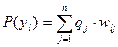
Тогда дополнительный выигрыш, который можно получить при проведении единичного эксперимента определяется следующим образом:

.

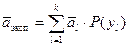Если 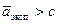, то эксперимент проводить стоит, если же наоборот, то не стоит.