Приемочный контроль. Условия выборочного контроля наиболее адекватно отражает гипергеометрический закон распределения, рассмотренный выше

Условия выборочного контроля наиболее адекватно отражает гипергеометрический закон распределения, рассмотренный выше. Два других закона используются для упрощенных оценок.

Решение о качестве партии изделий, принимаемой в результате выборочного контроля, требует определение объема выборки n при заданных уровне дефектности q и так называемом браковочным числе А_с.

С позиции теории, такое решение относят к решениям минимизирующим риск, и оно требует нахождения оперативной характеристики, которое определяется следующим образом:

F(q) = ∑P(n,z),

где F(q) – вероятность приемки партии изделий, среди которых доля дефектных изделий составляет q;

А_с – приемочное число (допустимое число дефектных изделий в выборке n);

P(n,z) – вероятности появления в выборке бракованных изделий, когда z последовательно принимает значения от 0 до А_с.

Иными словами это кумулятивная вероятность и ее можно определить по формуле:

∑ P(n,z) = P(60,0) + P(60,1) + З(60,2) + …З(60,20,

где n для примера принято равным 60, z заранее неизвестно и принято в диапазоне 0 – 20.

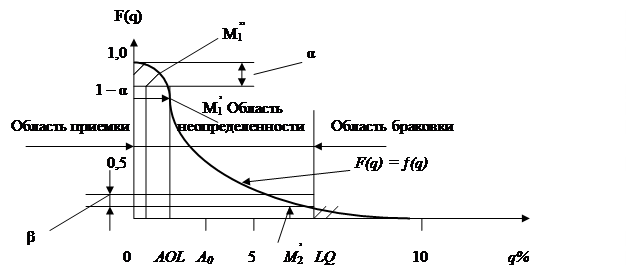
Оперативную характеристику можно представить в виде графика

F(q) =ƒ(q%), зафиксировав значение n, при заданных значениях A_c и N.

Например, используя гипергеометрический закон распределения при q от нуля до 10, при N = 1200; n = 100 и A_c = 3 получим:

C^A х С^n-A C³ x C^{100 - 3}

^{N N - N}_q ^{1200 1200 – q1200}

∑ P(n,z) = ———— = ———————,

Cⁿ Cⁿ

^{N N}

где N = 1200 – объем партии;

N_q = q x N – объем дефектных партий в партии.

Результаты расчетов приведены в таблице 10.6. Полученная оперативная характеристика контроля показана на рис. 10.4.

Таблица 10.6