Лучшее решение - это такое решение, когда критерий оптимизации принимает оптимальное значение, для
одних задач максимальное, для других –минимальное.
Решение управленческой задачи – это всегда выбор одного решения из возможных решений. Варианты решений определяются внешними и внутренними условиями, в которых действует организация. В этой связи говорят об области допустимых решений. В этих ограниченных условиях нужно выбрать лучшее решение. Лучшее решение - это такое решение, когда критерий оптимизации принимает оптимальное значение, для одних задач максимальное, для других – минимальное.
Начиная с 40-х годов ХХ века специально для нужд управления начали разрабатываться количественные методы принятия оптимальных решений. Новое научное направление получило название математическое программирование.
Математическое программирование объединяет методы нахождения оптимального значения целевой функции, переменные которой принадлежат некоторой области допустимых значений.
Задачу математического программирования можно записать в формализованном виде:
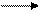 F(X) max(min) (9)
F(X) max(min) (9)
X Î M
где:
X = x1, x2, …, xn;
M – область допустимых значений переменных.
В зависимости о вида целевой функции и области допустимых значений переменных различают разные классы задач математического программирования. Так, если целевая функция линейна, а область допустимых решений задается системой линейных уравнений или неравенств, то рассматриваемая задача является задачей линейного программирования. Именно в области линейного программирования были сделаны первые успехи по оптимизации управленческих решений. Свое название математическое программирование получило от входящего в него линейного программирования, в котором наиболее ярко проявились специфические особенности нахождения экстремума (максимума или минимума) на границе области изменения переменных.
Сейчас в математическом программировании выделяют несколько характерных групп задач и методов их решения (по классификации академика Л.В. Канторовича):
Выпуклые задачи. Эти задачи решаются методами линейного и выпуклого программирования.
Невыпуклые задачи. При решении невыпуклой задачи с помощью методов локальных перемещений может быть найден локальный минимум.
Динамические задачи. Этот класс объединяет задачи с большим числом переменных, в которых выбор значений переменных производится последовательно и сделанные уже выборы сравнительно просто влияют на возможности выбора оставшихся переменных. В динамическом программировании решение одной большой задачи оптимизации распадается на большое число просто решаемых мелких задач.
Экстремальные задачи на сетях. Методы оптимизации на сетях в большинстве случаев являются вариантами методов линейного и динамического программирования.
Дискретные задачи. Здесь по условиям решения значения переменных должны быть целочисленными.
Наибольшее распространение в практике управления в настоящее время получили методы линейного программирования.
 2014-02-02
2014-02-02 752
752








