При взаимном вытеснении жидкостей

Кинематические условия на подвижной границе раздела

При изучении более сложных задач о вытеснении нефти водой, о явлении конусообразования, о влиянии изменения проницаемости пласта на поведение скважин и т.д. необходимо будет соответствующим образом усложнять рассмотренную простейшую схему пластовой водонапорной системы.

Рис. 9 является только общей схемой и не отображает ни точных деталей рельефа местности, ни более мелких особенностей геологической структуры XIII пласта. Из приведенных данных и из чертежа ясно видно, что разность гипсометрических отметок области питания А и области нефтеносности DBE вполне достаточна, чтобы объяснить величину начального пластового давления (порядка 60 ата на забоях нефтяных скважин на своде складки и до 80 ата на забоях наиболее глубоких крыльевых водяных скважин) и фонтанирование всех нефтяных и некоторых (с малыми альтитудами) водяных скважин.

Приведенные на рис. 6-9 схемы пластовых водонапорных систем наглядно поясняют происхождение артезианского напора: любая скважина, проведенная в области напора, например, в точке L рис. 6, в точках Е рис. 7-9, будет обладать свойством «восходимости», т.е. пьезометрический уровень жидкости в ней будет выше отметки кровли вблизи забоя скважины. Возможность самоизлива артезианских скважин определяется превышением гипсометрической отметки зеркала вод в области питания пласта над гипсометрической отметкой устья скважины (при условии, что потеря напора при естественном движении воды в условиях артезианского потока не слишком понижает пьезометрические уровни в области напора).

При анализе вертикальных разрезов (проведенных вдоль по падению пластов) типовых пластовых в донапорных систем легко заметить следующую важную характерную особенность: вертикальные их размеры значительно меньше горизонтальных. В самом деле, глубина залегания разрабатываемых водоносных и нефтеносных пластов редко превосходит 2-3 км, а протяжение пласта от его выходов на дневную поверхность до области разработки измеряется десятками, а иногда и сотнями километров. При гидродинамическом решении очень многих задач подземной гидромеханики: при выяснении особенностей работы отдельных скважин, при решении проблемы взаимодействия скважин, при выяснении законов изменения пластового давления в области нефтеносности в зависимости от темпов отбора жидкости и т.д. — вполне допустима некоторая схематизация строения пластовой водонапорной системы от области разработки до области питания.

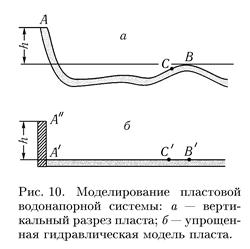Допустим, например, что пластовая водонапорная система имеет в вертикальном разрезе форму, представленную на рис. 10, а. Буквой А отмечено положение зеркала воды в области питания. На своде складки В расположена разрабатываемая залежь нефти, газа и воды. Разность h высотных отметок А и В определяет пластовое давление в точке В (При наличии в пласте естественного артезианского потока следует учесть падение напора в пласте, вызванное движением вод).

На рис. 10, б в вертикальном разрезе представлена упрощенная схема той же пластовой водонапорной системы. Сосуд А'А", в котором уровень воды расположен на высоте h над точкой В' заменяет область питания; участок пласта А'С'В' взят горизонтальным. Длину участка А'С'В' (рис. 10, б) можно взять либо равной расстоянию между участками А и на рис. 10, а, измеренному в горизонтальном направлении, либо можно учесть истинную длину участка АСВ, измеренную вдоль пласта. Следует иметь в виду, что в большинстве случаев в гидродинамические формулы расстояние А'' от скважин до области питания входит под знаком логарифма. Поэтому ошибки в оценке величины этого расстояния даже на 100-200% весьма мало отражаются на результатах гидродинамических подсчетов.

В некоторых случаях, упрощая задачу, допустимо «спрямлять пласт» лишь на участке АС, но на участке СВ следует сохранять его естественный уклон; с таким случаем приходится сталкиваться, например, при разработке залежи нефти на круто падающем крыле антиклинальной складки (считая, что СВ — крыльевой нефтеносный участок, С — отметка начального зеркала воды).

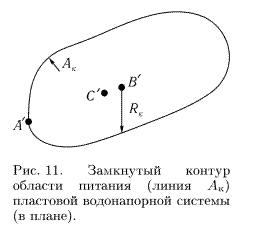Предположим, что область питания охватывает пласт со всех сторон соответствующая типовая схема представлена на рис. 6; тогда граница области питания представится в плане замкнутым контуром. Сохраняя это предположение и проводя на рис. 10, б горизонтальное сечение по кровле «пласта» А'В'С получим на рис. 11 изображение в плане схематизированной пластовой водонапорной системы (ради сокращения размеров чертежа на рис. 11 размеры уменьшены в два раза по сравнению с рис. 10, б). Замкнутый контур А_к соответствует внутренней границе сосуда, изображающего области питания. Итак, контур А_к отделяет область питания от области напора схематизированной пластовой водонапорной системы. Давление вдоль контура А_к определяется высотой h уровня жидкости в области питания.

Во всех случаях, когда описанная схематизация допустима, условимся линию А_к называть «контуром области питания»; если точка В' лежит, примерно, в центре области ограниченной линией А_к, то среднее расстояние от В' до точек контура А_к будем называть «средним радиусом контура области питания».

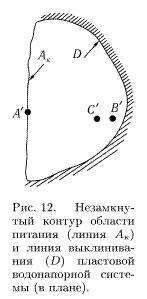Если изображенная на рис. 10, а пластовая водонапорная система имеет область питания лишь со стороны А, а со стороны В пласт выклинивается, то, проводя опять горизонтальное сечение по линии А'С'В' рис. 10, б, получим новое изображение в плане схематизированной пластовой водонапорной системы (рис. 12).

На рис. 12 линия А_к представляет собой контур области питания, а заштрихованная линия D — непроницаемую границу пласта (линию выклинивания).

Моделирование пластовых водонапорных систем по образцу схемы, (рис. 10, б), позволяет с достаточным приближением к действительности довести до конца гидродинамическое решение очень многих задач подземной гидромеханики. Рассмотренные выше модели и схемы пластовых водонапорных систем будут вполне приемлемы и для анализа поведения нефтеводоносного пласта в условиях упругого режима.

Основная трудность точного решения задачи о движении границы раздела двух жидкостей в пористой среде заключается в том, что линии тока на границе раздела жидкостей преломляются.

Пусть кривая 1-1 (рис. 9.1) служит границей раздела двух жидкостей с вязкостями μ₁ и μ₂ и пусть, например, μ₂ > μ₁ (нефть (μ_н2 = 28 мПа·с) вытесняется водой (μ_в1 = 1 мПА·с)).

Рассмотрим произвольную точку М границы 1-1 и проведем через нее касательную τ и нормаль n к границе раздела жидкостей 1-1. Найдем проекции скоростей фильтрации воды и нефти, находящихся в данный момент в точке М, на касательную и нормаль, считая проницаемость пористой среды k постоянной по обе стороны границы раздела.

Согласно неразрывности потока массы элементарные расходы обеих несжимаемых жидкостей через элемент границы раздела, включающий точку М, должны быть равны между собой. Отсюда следует, что нормальные составляющие скоростей фильтрации обеих жидкостей будут равны, т. е. ω_1n = ω_2n.

Давление в пласте в точке М также должно быть одинаково для обеих жидкостей, так как при малых скоростях (ниже звуковых) разрыва давления в сплошном потоке быть не может.

Касательные составляющие скоростей фильтрации обеих жидкостей будут определяться по закону Дарси:

, (9.1)

Так как μ₂ > μ₁, то из (9.1) получаем, что ω_1n > ω_2n. Отсюда следует, что результирующий вектор скорости фильтрации ω₁ = ω_1n + ω_1τ, касательный к линии тока МА, будет больше вектора ¯ω₂ = ω_2n + ω_2τ, касательного к линии тока MB. Следовательно, линии тока AM и MB, проходящие через точку М, будут иметь излом в точке М.

Учет этого преломления линий тока на границе раздела жидкостей и составляет главную трудность в точном решении задачи продвижения границы раздела.

Линии тока не будут преломляться только в двух случаях – при прямолинейно-параллельном и плоскорадиальном движениях границы раздела, когда ω_1τ = ω_2τ = 0.

Примем условие, что разновязкие жидкости (нефть и вода) несмешивающимися, взаимно нерастворимыми и химически не реагирующими одна с другой и с пористой средой.

Вытеснение нефти водой предполагается происходящим полностью - так называемое «поршневое» вытеснение.