МР =
= 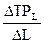 =
= 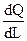
Аналогично рассчитывается предельный продукт от капитала и других факторов производства
МР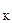 =
= 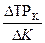 и т.п.
и т.п.
Средний продукт – общий продукт, приходящийся на единицу задействованного переменного фактора. Средний продукт труда можно определить как
АР =
= 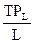 =
= 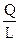
Аналогично, средний продукт капитала определяется по формуле
АР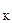 =
= 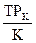 ;
;
Взаимосвязь общего, среднего и предельного продукта какого-либо фактора производства определяется действием закона убывающей предельной отдачи фактора производства.
При выборе способа производства фирма должна учитывать изменение не только предельного продукта, но и изменение среднего продукта. Кривые среднего и предельного продукта пересекаются в точке максимума среднего продукта.
Изокванты. Предельная норма технического замещения.
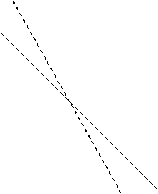
Термин «изокванта» означает одинаковое количество продукции, т.е. изокванте принадлежат любые комбинации труда и капитала, которые позволяют фирме производить то же самое количество продукции.
При фиксированном Q производственной функции Q = f(L, K) соответствует определенная изокванта.
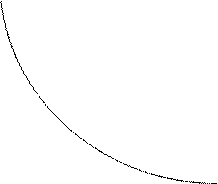 Изокванта – это «кривая безразличия» для производственной функции. Семейство изоквант показано
Изокванта – это «кривая безразличия» для производственной функции. Семейство изоквант показано
 |
 К
К
 |


 А Q
А Q

 В Q
В Q
Q

 L
L
 α
α  β
β
Важнейшая характеристика изокванты – предельная норма технического замещения или MRTS.
Если отложить труд (L) по горизонтали, капитал (К) по вертикали, то
MRTS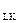 = -
= - 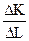 |
| или MRTS
или MRTS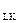 = -
= - 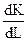 , где К = φ(L,
, где К = φ(L, 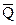 ).
).
Здесь 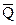 - фиксированный выпуск продукции.
- фиксированный выпуск продукции.
MRTS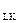 - это норма, в которой количество капитала может быть уменьшено при увеличении количества труда на 1 единицу, при этом выпуск продукции остается неизменным.
- это норма, в которой количество капитала может быть уменьшено при увеличении количества труда на 1 единицу, при этом выпуск продукции остается неизменным.
MRTS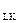 = -
= - 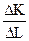 =
= 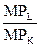
При движении вдоль изокванты сверху вниз MRTS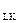 убывает, или, что эквивалентно, изокванта является выпуклой к началу координат. Убывание предельной нормы технического замещения связано с законом убывающей предельной отдачи, т.к. именно этот закон определяет изменение величин MP
убывает, или, что эквивалентно, изокванта является выпуклой к началу координат. Убывание предельной нормы технического замещения связано с законом убывающей предельной отдачи, т.к. именно этот закон определяет изменение величин MP и МР
и МР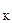 при изменении L и К.
при изменении L и К.
Эластичность замещения (σ) измеряет, как быстро предельная норам технического замещения капитала трудом (MRTS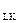 ) изменяется при движении вдоль изокванты.
) изменяется при движении вдоль изокванты.
Эластичность замещения (σ) может быть рассчитана по формуле:
σ = 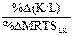 =
= 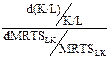 .
.
Очевидно, σ ≥ 0. Если замещение капитала трудом осуществляется трудно (с технической точки зрения), тогда процентное изменение в MRTS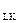 при движении вдоль изокванты будет значительным и величина σ будет близка к нулю.
при движении вдоль изокванты будет значительным и величина σ будет близка к нулю.
Если замещение капитала трудом осуществляется легко, то процентное изменение в MRTS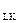 будет незначительным и величина σ будет большой.
будет незначительным и величина σ будет большой.
Можно сказать, что коэффициент σ определяет меру кривизны изокванты.
Связь между выпуском продукции и минимально возможными затратами, необходимыми для его обеспечения, называется функцией издержек – ТС.
В общем виде TC(Q) = f[Q(L, K), P , P
, P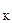 ], где Р
], где Р - почасовая оплата труда, Р
- почасовая оплата труда, Р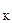 - почасовая оплата работы капитала (оборудования) или арендная плата.
- почасовая оплата работы капитала (оборудования) или арендная плата.
Часто используют следующие обозначения: Р = w, P
= w, P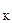 = r.
= r.
При заданных ценах ресурсов функцию издержек можно представить в виде: ТС = w·L + r·K.
Изокостойназывается линия затрат, отражающая сочетания труда и капитала, при которых издержки производства равны (остаются неизменными).
Наклон изокосты равен - 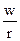 .
.
При анализе поведения фирмы различаются 2 периода – долгосрочный и краткосрочный. В долгосрочном все ресурсы являются переменными, в краткосрочном – некоторые из ресурсов постоянны.
Оптимальная комбинация используемых ресурсов в долгосрочном периоде.
В общем виде задача минимизации издержек выглядит так:
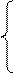 TC(Q) = (w·L + r·K)
TC(Q) = (w·L + r·K) 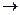
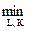
f(L, K) = Q, где Q – фиксированный выпуск
L, K ≥ 0
Для нахождения оптимального способа производства должны выполняться следующие условия:
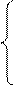 MRTS
MRTS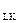 =
= 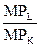 =
= 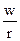
f(L, K) = Q
L, K ≥ 0
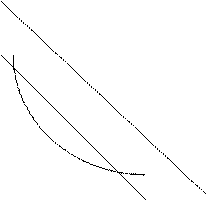
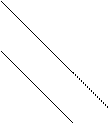
Графически:
 К
К
 |
A
 |

 K E
K E
B
 Q =
Q = 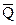
L L
искомая изокоста: наклон = -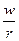 ; в точке касания Е значение издержек производства минимально; наклон изокванты в т. Е равен -
; в точке касания Е значение издержек производства минимально; наклон изокванты в т. Е равен -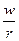
Способы производства А и В являются технически эффективными, но не оптимальными, т.к. они находятся на изокосте, соответствующей более высокому уровню затрат, чем изокоста, проходящая через т. Е. Двигаясь от т. А к т. Е, фирма может произвести то же количество продукции 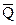 , но при более низких затратах. Следовательно, единственно оптимальным решением является т. Е. Только в точке касания заданной изокванты и изокосты выполняется равенство:
, но при более низких затратах. Следовательно, единственно оптимальным решением является т. Е. Только в точке касания заданной изокванты и изокосты выполняется равенство:
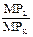 =
= 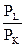 =
= 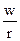 .
.
Отдача от масштаба. Когда факторы производства имеют положительные предельные продукты, общий выпуск должен расти при увеличении затрачиваемых факторов производства. Это означает, что масштаб деятельности фирмы увеличился. Отдача от масштаба показывает, на сколько процентов увеличился выпуск продукции, когда фирма увеличивает использование всех факторов производства на заданный процент:
Отдача от масштаба = 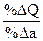 (а – количества всех факторов производства).
(а – количества всех факторов производства).
Допустим, фирма использует два ресурса – труд (L) и капитал (К), чтобы произвести выпуск в количестве Q, т.е. Q = f(L, K). Предположим, что все используемые фирмой ресурсы увеличились в λ раз (λ > 1), т.е. количество используемого труда увеличилось с L до λL, капитала – с К до λК. Пусть ψ представляет итоговый рост выпуска, т.е. выпуск увеличился с Q до ψQ. Тогда:
· Если ψ > λ, мы имеем возрастающую отдачу от масштаба.
· Если ψ = λ, мы имеем постоянную отдачу от масштаба.
· Если ψ < λ, мы имеем убывающую отдачу от масштаба.
С возрастающей отдачей от масштаба непосредственно связана экономия от масштаба - снижение издержек на единицу продукции по мере увеличения масштаба производства. Может быть обусловлена рядом факторов: во-первых, специализацией и разделением труда, во-вторых, неделимостью ресурсов, в-третьих, так называемым «принципом контейнера, в-четвертых, большей эффективностью крупного оборудования и т.д.
В то же время наблюдается не только экономия от масштаба, но и потери от масштаба- снижение издержек на единицу продукции по мере увеличения масштаба производства.
Оптимальная комбинация ресурсов: подход на основе предельного продукта.
Если рассматривать упрощенную модель с двумя видами ресурсов (трудом и капиталом), то минимизирующая издержки их комбинация должна удовлетворять условию: 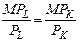 , где MP L – предельный продукт труда (прирост продукции на дополнительную единицу применяемого труда), P L – цена единицы труда, MP K – предельный продукт капитала (прирост продукции на дополнительную единицу применяемого капитала), P K – цена единицы капитала. Равенство говорит нам о том, дополнительная продукция с последней затраченной на каждый ресурс денежной единицы должна быть одинакова.
, где MP L – предельный продукт труда (прирост продукции на дополнительную единицу применяемого труда), P L – цена единицы труда, MP K – предельный продукт капитала (прирост продукции на дополнительную единицу применяемого капитала), P K – цена единицы капитала. Равенство говорит нам о том, дополнительная продукция с последней затраченной на каждый ресурс денежной единицы должна быть одинакова.
Производственная эффективность есть такая комбинация ресурсов, которая минимизирует издержки на данный объем продукции. В общем случае, для ряда ресурсов, производственная эффективность можно представить как:
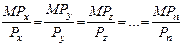
Оптимальная комбинация ресурсов: подход с использованием изоквант и изокосты.
 K
K
 N
N
 |
 R
R

 A
A

 F
F
 Q = Q
Q = Q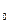
 L
L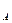 H L
H L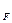 M L
M L
Оптимальной комбинацией ресурсов будет являться точка А, в которой изокванта касается изокосты.
Тема 6 - Концентрация капитала и рыночная власть
План лекции:
1 Понятие издержек. Виды издержек производства.
2 Функция издержек и производственная функция.
3 Издержки производства в краткосрочном периоде.
4 Издержки в долгосрочном периоде.
Экономисты выделяют два вида издержек: явные и неявные (вмененные).
К явным издержкам относятся фактические затраты и амортизационные отчисления по капитальному оборудованию.
 2014-02-02
2014-02-02 4401
4401