Цель и задача управления
ТЕМА 3 ОСНОВНЫЕ ПОНЯТИЯ И ТИПЫ ЗАДАЧ УПРАВЛЕНИЯ
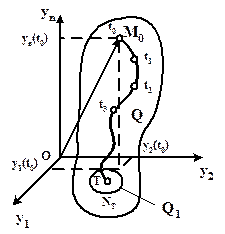 |
Пусть в начальный момент времени
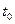 начало вектора состояния
начало вектора состояния 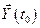 находится в точке
находится в точке 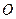 , а конец – в точке
, а конец – в точке 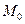 (рис. 3.1). За время
(рис. 3.1). За время 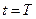 объект должен перейти в точку
объект должен перейти в точку 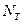 . Отметим эти точки в фазовом пространстве (пространстве состояний) - системе координат, по осям которой отложены координаты вектора состояний
. Отметим эти точки в фазовом пространстве (пространстве состояний) - системе координат, по осям которой отложены координаты вектора состояний 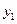 ,
, 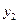 , …,
, …, 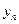 (например, для трёхмерного пространства
(например, для трёхмерного пространства 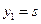 ,
, 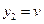 ,
, 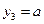 ).
). Рисунок 3.1 – Траектория движения объекта в фазовом пространстве
Если в каждый момент времени 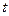 , отложить в фазовом пространстве точку, соответствующую вектору
, отложить в фазовом пространстве точку, соответствующую вектору 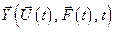 , то получим траекторию движения объекта.
, то получим траекторию движения объекта.
Траекторией движения объекта называется след, оставляемый вектором состояния в фазовом пространстве с течением времени.
В силу конструктивных, прочностных, энергетических и других особенностей управляющее воздействие не может превышать какой - то величины 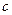 , т.е.
, т.е.
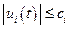 , (3.1)
, (3.1)
где 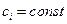 ;
; 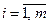 .
.
Область возможных значений управляющих воздействий 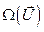 называют областью допустимых управлений. Реально подаваемые на вход ОУ управления должны принадлежать области допустимых управлений, сокращённо
называют областью допустимых управлений. Реально подаваемые на вход ОУ управления должны принадлежать области допустимых управлений, сокращённо
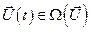 . (3.2)
. (3.2)
Аналогично компоненты вектора состояния 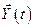 в общем случае также должны удовлетворять определённым ограничениям. Некоторая область
в общем случае также должны удовлетворять определённым ограничениям. Некоторая область 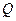 в пространстве состояний, за пределы которой не должен выходить вектор состояний
в пространстве состояний, за пределы которой не должен выходить вектор состояний 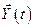 называется областью допустимых состояний, сокращённо
называется областью допустимых состояний, сокращённо
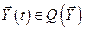 . (3.3)
. (3.3)
В области допустимых состояний 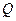 можно выделить подобласть
можно выделить подобласть 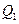 , в пределах которой по каким-то причинам значения вектора состояния в конечный момент времени
, в пределах которой по каким-то причинам значения вектора состояния в конечный момент времени 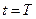 будет желательным (см. рис. 3.1).
будет желательным (см. рис. 3.1).
Цель управления – перевести объект из начального состояния 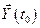 в конечное
в конечное 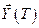 , принадлежащее подобласти (
, принадлежащее подобласти (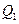 ) желаемых значений вектора состояния, находящейся в области допустимых состояний
) желаемых значений вектора состояния, находящейся в области допустимых состояний 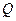 . При этом конечное время
. При этом конечное время  может быть неизвестно. Для достижения цели управления на вход ОУ необходимо подать соответствующее управление.
может быть неизвестно. Для достижения цели управления на вход ОУ необходимо подать соответствующее управление.
Задача управления - в области допустимых управлений 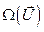 подобрать такое управление, при котором будет реализована цель управления, т.е. найти такое допустимое управление
подобрать такое управление, при котором будет реализована цель управления, т.е. найти такое допустимое управление 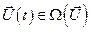 на временном отрезке
на временном отрезке  , при котором уравнения состояния ОУ в конечный момент времени
, при котором уравнения состояния ОУ в конечный момент времени  при заданном начальном состоянии
при заданном начальном состоянии 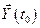 имеют решения, находящиеся в области желаемых значений
имеют решения, находящиеся в области желаемых значений 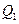 .
.
3.2 Критерии качества
Как правило, задача управления имеет большое число решений. Однако к системе управления часто предъявляется ряд требований, не описанных в задаче управления (например, быстрее, с наименьшими затратами и т.д.). Для оценки степени соответствия системы, предъявляемым требованиям, вводятся числовые показатели, характеризующие качество управления.
Качество управления можно характеризовать двумя способами:
1) в форме совокупности показателей качества (время, затраты, площадь, …);
2) в форме некоторого обобщённого показателя (время достижения цели, значение максимальной ошибки, безотказность работы, производительность, себестоимость и т.д. – для каждого случая своего).
Наиболее часто обобщенный показатель качества управления  можно представить в виде функционала:
можно представить в виде функционала:
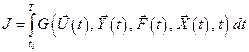 (3.4)
(3.4)
где 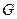 – функция, определяющая конкретный физический смысл показателя качества
– функция, определяющая конкретный физический смысл показателя качества  . Тогда задача оптимального управления может быть сформулирована следующим образом: при переводе объекта управления из начального состояния
. Тогда задача оптимального управления может быть сформулирована следующим образом: при переводе объекта управления из начального состояния 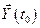 в конечное
в конечное 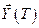 , оставаясь в области допустимых состояний
, оставаясь в области допустимых состояний 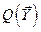 на всём временном отрезке
на всём временном отрезке 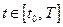 , найти в области допустимых управлений
, найти в области допустимых управлений 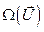 такое управление
такое управление  , при котором показатель
, при котором показатель  достигает экстремального (оптимального) значения:
достигает экстремального (оптимального) значения:
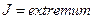 . (3.5)
. (3.5)
Условие (3.5) называется критерием оптимальности.
Управление, реализуемое критерий оптимальности называется оптимальным; систему управлений, которая с позиции критерия оптимальности является наилучшей, называют оптимальной.
Пусть на управление  не наложены ограничения (3.1). Тогда объект называется управляемым, если можно подобрать такое управление
не наложены ограничения (3.1). Тогда объект называется управляемым, если можно подобрать такое управление  , с помощью которого объект будет переведён из начального состояния
, с помощью которого объект будет переведён из начального состояния 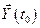 , в конечное
, в конечное 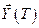 за конечное время
за конечное время 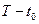 . Другими словами, вектор управления
. Другими словами, вектор управления  должен влиять на все компоненты вектора состояния
должен влиять на все компоненты вектора состояния 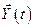 .
.
Если на вектор управления  налаживаются ограничения, например (3.1), то полностью управляемый объект может стать неуправляемым. Таким образом, понятие управляемости отвечает на вопрос: возможно ли существование оптимального управления для данного объекта при конкретных ограничениях и начальных состояниях. Соответствующие исследования проводятся с использованием понятия достижимости.
налаживаются ограничения, например (3.1), то полностью управляемый объект может стать неуправляемым. Таким образом, понятие управляемости отвечает на вопрос: возможно ли существование оптимального управления для данного объекта при конкретных ограничениях и начальных состояниях. Соответствующие исследования проводятся с использованием понятия достижимости.
Конечное состояние 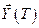 является достижимым из исходного состояния
является достижимым из исходного состояния 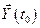 , если найдётся такое управление
, если найдётся такое управление  из области допустимых управлений
из области допустимых управлений 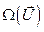 , при котором объект за конечное время
, при котором объект за конечное время 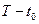 будет переведён из исходного состояния
будет переведён из исходного состояния 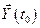 в конечное состояние
в конечное состояние 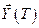 . Совокупность достижимых состояний
. Совокупность достижимых состояний 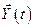 образует область достижимых состояний
образует область достижимых состояний 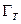 в момент времени
в момент времени  из исходного состояния
из исходного состояния 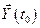 по отношению к области допустимых управлений
по отношению к области допустимых управлений 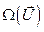 .
.
Задача оптимального управления имеет смысл, если конечное состояние объекта 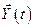 принадлежит области допустимых состояний
принадлежит области допустимых состояний 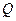 . В большинстве технических задач конечное состояние
. В большинстве технических задач конечное состояние 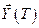 является достижимым, а объект - управляемым.
является достижимым, а объект - управляемым.
Ранее мы считали, что известно начальное состояние 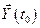 . Но на практике не всегда вектор состояния
. Но на практике не всегда вектор состояния 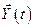 можно измерить (обычно измеряется
можно измерить (обычно измеряется  и
и 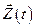 ). Поэтому, наблюдая за выходными
). Поэтому, наблюдая за выходными 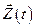 и входными
и входными  параметрами объекта управления в течение времени
параметрами объекта управления в течение времени  , можно определить начальное состояние объекта
, можно определить начальное состояние объекта 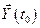 .
.
Наблюдаемостью называется возможность восстанавливать начальное состояние объекта 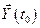 по наблюдениям за выходом
по наблюдениям за выходом 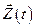 и входом
и входом  в течение конечного отрезка времени
в течение конечного отрезка времени  . Состояние
. Состояние 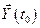 называется наблюдаемым, если при заданном управлении
называется наблюдаемым, если при заданном управлении  существует такой конечный промежуток времени
существует такой конечный промежуток времени 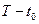 , на котором, зная вход
, на котором, зная вход  и выход
и выход 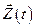 объекта управления на этом промежутке, можно определить начальное состояние
объекта управления на этом промежутке, можно определить начальное состояние 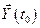 .
.
 2014-02-04
2014-02-04 1788
1788








