Основы вариационного исчисления

ТЕМА 4 МЕТОДЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

1. Какое пространство называется фазовым? Что представляет собой траектория движения объекта?

2. Каким образом можно объяснить понятия: область допустимых управлений, область допустимых состояний, область желаемых состояний?

3. Какие цель и задача управления?

4. Какая причина введения понятия показателя качества? В каких формах он может использоваться?

5. Как формулируется задача оптимального управления с учётом показателя качества? Какое используется условие для критерия оптимальности?

6. Каким образом можно объяснить понятия: управляемость, достижимость, наблюдаемость?

7. Как классифицируются задачи оптимального управления?

8. Какие примеры задач оптимального управления приводятся в конспекте лекций? Как определяется критерий оптимальности в каждом случае?

Вариационное исчисление – раздел математики, занимающийся поисками функций, на которых некоторые величины достигаю максимума или минимума. Если каждой функции можно сопоставить число , то является функционалом функции , т.е. 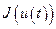. Другими словами, функционал является функцией, у которой аргумент является функцией.

Рассмотрим простейшую задачу вариационного исчисления.

Пусть задан функционал с известными пределами интегрирования 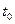и :

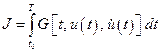(4.1)

Если функция 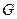однозначна и непрерывна вместе со своими частными производными до второго порядка, а функция однозначна и непрерывна вместе с производными первого порядка, то такие функции называются гладкими. Обозначим гладкие функции .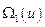

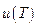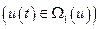Если заданные значения функции в начальной и конечной точках и сама функция является гладкой , то такая функция называется допустимой.

Тогда задача вариационного исчисления формулируется следующим образом: среди допустимых функций 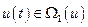найти такую функцию, на которой функционал (4.1) достигает наименьшего значения. Математически это условие можно записать в следующей форме:

. (4.2)

Функционал 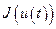достигает на кривой 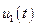минимума, если его значение на любой другой кривой 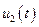, близкой к этой кривой 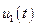, не меньше, чем на 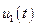, т.е.

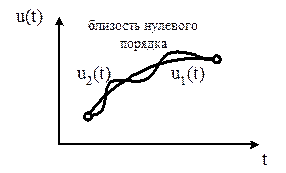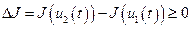Часто при решении задач, описываемых с помощью дифференциальных уравнений, получается несколько близких функций, но только одна из них будет оптимальной (наилучшей). Поэтому рассмотрим понятие близости.

Две функци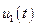и и 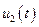называются близкими в смысле близости нулевого порядка, если максимальное значение модуля разности функций мало:

где 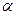– достаточно малое число.

Рисунок 4.1 – Близость функций нулевого порядка (сильный минимум)

Две функци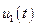и и 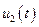называются близкими в смысле близости первого порядка, если мало не только максимальное значение модуля разности функций, но и максимальное значение модуля разности первых производных функций, т.е.

, .

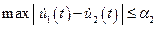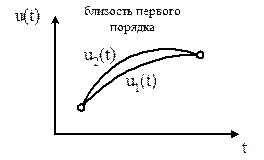Рисунок 4.2 – Близость функций первого порядка (слабый минимум)

Аналогичные определения можно дать и для близости функций более высоких порядков (для второго, …, -того порядков).

Для функционала (4.1) необходимо сравнивать допустимые функции в смысле близости первого порядка, так как 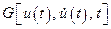является функцией от первой производной по управлению .

Если функционал 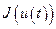достигает на кривой 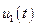минимума по отношению ко всем остальным кривым, близким к 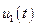в смысле близости нулевого порядка, то такой минимум называется сильным. В этом случае минимальная функция выбирается среди многих близких кривых, для которых выполняется лишь одно условие .

Если функционал 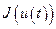достигает на кривой 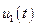минимума по отношению к кривым, близким к 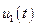в смысле близости первого порядка, то такой минимум называется слабым. Здесь минимальная функция выбирается среди немногих кривых, для которых выполняется и условие , и условие 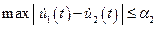. Следовательно, условие сильного минимума входит в условие слабого минимума. Отсюда видно, что сильный минимум является и слабым (но не наоборот).

В задачах мы будем искать только слабый минимум.