Примеры задач оптимального управления

Классификация задач оптимального управления

В общем случае задачи оптимального управления можно разделить на два больших класса:

- задачи оптимального программного управления;

- задачи синтеза оптимального управления.

Если оптимальное управление зависит только от времени 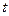, то такая задача называется задачей оптимального программного управления (для разомкнутой системы без обратной связи). Для замкнутых систем (с каналом обратной связи и компенсацией возмущений) оптимальное управление зависит от векторов состояния 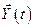, задающего воздействия 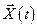и возмущения 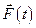, т.е. . Такие задачи называются задачами синтеза оптимального управления.

По ограничениям на состояние ОУ и время управления задачи делятся на следующие:

1) задачи с фиксированным временем (только конечное время является известной фиксированной величиной);

2) задачи со свободным правым концом. Здесь фиксируется конечный момент времени , а ограничения на конечное положение вектора состояния 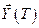снимаются;

3) задачи без ограничения на переменные состояния всего вектора 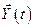(ограничения (3.3) снимаются, и переменные состояния 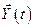принадлежат всему пространству состояния; конечное время может быть любым);

4) задачи с закреплённым правым концом траектории. В этих случаях подмножество желаемых значений 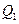представляет собой единственную точку, в которую должен попасть вектор 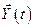в конечный момент времени 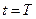. В противном случае, (если 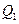- подобласть пространства состояний, а не единственная точка) используется термин «задачи с подвижным правым концом».

1. Задача о минимальной длительности переходного процесса.

В электронных цепях при наличии коммутационных устройств и ёмкостных или индукционных элементов возникают переходные процессы, временную зависимость которых можно изобразить с помощью графика, представленного на рис. 3.2.

Рисунок 3.2 – Переходной процесс

Для стабильной работы электронных схем переходные процессы в основном являются нежелательными и поэтому стремятся к уменьшению длительности переходных процессов. Сформулируем задачу оптимального управления для этого случая.

Пусть имеется система управления, структура которой представлена на рис. 1.2. Объект управления в начальный момент времени 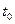находится в нулевом состоянии 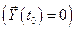. На вход системы подаётся задающее воздействие в форме единичной ступенчатой функции 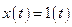. Необходимо найти такое управление 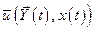, при котором переход вектора состояния 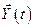из начального состояния 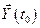в конечное 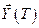с учётом ограничения (3.1) займёт минимальное время.

В этом случае критерий оптимальности примет вид:

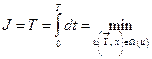Широкий класс задач оптимального управления, в которых необходимо найти минимальное время какого-нибудь процесса, называется задачами о максимальном быстродействии.

2. Задача о максимальной точности воспроизведения.

При серийном производстве изделий необходимо, чтобы они как можно более точно соответствовали образцу. Однако различные внешние случайные факторы являются причиной возникновения отклонений от образца. Класс задач оптимального управления, позволяющих определить режимы производства изделий с наименьшим отклонением от образцов, называется задачами о максимальной точности воспроизведения. Сформулируем такую задачу.

Пусть на УУ подаётся задающее воздействие 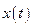, которое воспроизводится на выходе ОУ, т.е. . На ОУ действует случайное возмущение 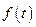, вероятные свойства которого известны. Такое возмущение 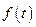приведёт к отклонению выходной переменной 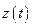от заданной величины 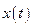на ошибку 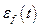, т.е. . Необходимо подобрать такую импульсную характеристику УУ, что бы среднеквадратичная ошибка 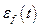выходного сигнала 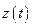, вызванная возмущением 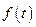, была бы минимальной.

Критерий оптимальности для такой задачи можно записать следующим образом:

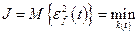3. Задача об оптимизации конечного состояния.

Рассмотрим на примере ракеты. Пусть ракета массой 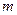с запасом топлива поднимается на высоту , расходуя топливо с секундным расходом 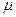. Учитывая ускорение свободного падения 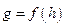, силу лобового сопротивления 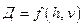и коэффициента пропорциональности между тягой двигателя и расходом топлива 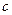, подобрать такой секундный расход топлива 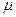, чтобы ракета за конечное время (неизвестное) поднималась на максимальную высоту .

Обозначим высоту 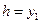, скорость полета 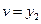, массу _.

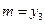Тогда ;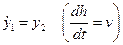

Согласно второму закону Ньютона ускорение

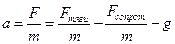Запишем это выражение с учётом условия задачи:

Заменим физические величины переменными состояния

;

Критерий оптимальности можно записать в виде условия:

при дополнительных ограничениях

; ; ; .

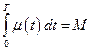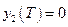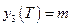Тогда задачу оптимизации конечного состояния можно сформулировать следующим образом: в области допустимых управлений 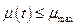найти такое управление 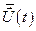, чтобы одна из переменных состояния (например, высота 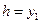) в конечный момент времени принимала максимальное значение. Задачи такого типа называются терминальными.

4. Задача о минимальном расходе топлива.

Иначе предыдущую задачу можно сформулировать таким образом: найти такой расход топлива 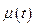, при ограничении 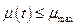, при котором количество топлива, затраченное на подъём на высоту , оказалось бы минимальным, т.е.

5. Задача о минимальных энергетических затратах.

Пусть под действием управления объект перемещается из начального в конечное состояние и описывается уравнениями состояния ; . Необходимо найти такое управляющее воздействие 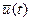, чтобы энергетические затраты на перемещение объекта за время были бы минимальными.