Условия Лежандра

Условие экстремальности (4.6) является необходимым, но не достаточным условием для нахождения оптимального управления, так как 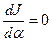не только для экстремальных значений функционала 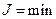или 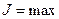, но и для точек перегиба (рис. 4.3).

Рисунок 4.3 – Точки перегиба

Для того чтобы функционал принимал минимальное значение необходимо, чтобы выполнялось условие 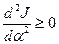, для максимального значения - условие .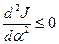

Найдём .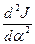

Учитывая, что функционал задаётся выражением (4.3), можно записать:

.

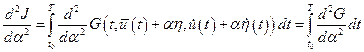Так как 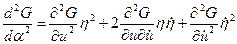, то

.

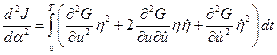Найдём среднее слагаемое .

Воспользуемся свойствами интегралов (4.4) .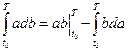

Обозначим ; .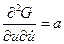

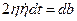Тогда ; ; .

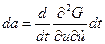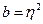В результате получим, что

.

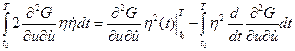С учётом того, что , получим

. (4.8)

Проанализируем полученное выражение (4.8) для минимального значения функционала (т.е. при ).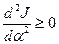

Так как первое слагаемое в выражении (4.8) 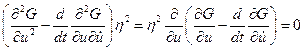, согласно уравнению Эйлера (4.6), то 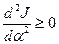при

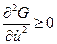. (4.9)

Полученное условие минимальности функционала (4.9) называется необходимым условием Лежандра, которое формулируется следующим образом: для достижения на некоторой экстремали минимума функционала необходимо, чтобы во всех точках этой экстремали выполнялось условие (4.9); для достижения максимума

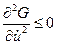. (4.10)

При условии 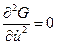экстремаль испытывает изломы.

Таким образом, уравнение Эйлера (4.6) и условия Лежандра (4.9), (4.10) являются необходимыми условиями для экстремума функционала.

Кроме необходимых условий, существуют и достаточные условия экстремальности функции:

1) функция должна удовлетворять уравнению Эйлера (4.6), т.е. должна являться экстремалью;

2) на экстремали должны выполняться условия Лежандра (4.9), (4.10);

3) уравнение Якоби

должно иметь решение , удовлетворяющее условию и не превращаться в нуль ни в одной точке при .