Ранее мы считали, что точки 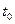 ,
,  ,
,  и
и 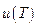 заданы (см. определение допустимой функции). Но в ряде случаев они могут быть неизвестными. Тогда рассмотрим методику решения задач, в которых необходимо подобрать такую функцию
заданы (см. определение допустимой функции). Но в ряде случаев они могут быть неизвестными. Тогда рассмотрим методику решения задач, в которых необходимо подобрать такую функцию 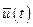 , чтобы функционал
, чтобы функционал 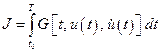 принимал наименьшее значение.
принимал наименьшее значение.
Для нахождения пяти неизвестных величин 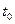 ,
,  ,
,  ,
, 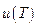 и
и  необходимо пять уравнений.
необходимо пять уравнений.
Функцию 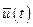 можно найти из уравнения Эйлера (4.6):
можно найти из уравнения Эйлера (4.6):
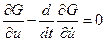 . (4.14)
. (4.14)
Четыре другие неизвестные можно найти из равенства нулю первых производных:
- для нахождения  используется условие
используется условие
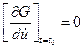 ; (4.15)
; (4.15)
- для нахождения 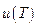 используется условие
используется условие
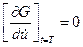 ; (4.16)
; (4.16)
- для нахождения 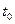 - условие
- условие
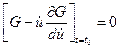 ; (4.17)
; (4.17)
- для нахождения  - условие
- условие
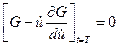 ; (4.18)
; (4.18)
Условия (4.15)-(4.18) называются условиями трансверсальности.
Методика нахождения 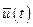 ,
, 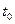 ,
,  ,
,  и
и 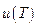 следующая: решив уравнение (4.14) получаем функцию
следующая: решив уравнение (4.14) получаем функцию 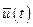 с постоянными интегрирования
с постоянными интегрирования 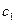 и
и 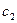 . Подставляя полученную функцию
. Подставляя полученную функцию 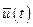 в условия трансверсальности (4.15)-(4.18), находим постоянные интегрирования
в условия трансверсальности (4.15)-(4.18), находим постоянные интегрирования 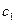 ,
, 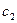 , и
, и 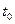 ,
,  .
.
В ряде задач требуется найти оптимальное решение 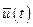 в предположении, что начало и конец решения лежат на некоторых заданных кривых, т.е.
в предположении, что начало и конец решения лежат на некоторых заданных кривых, т.е.
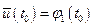 ;
; 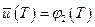 , (4.19)
, (4.19)
где 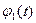 и
и 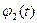 - известные функции, а
- известные функции, а 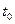 ,
,  - неизвестные величины.
- неизвестные величины.
Тогда для минимизации функционала  необходимо найти только
необходимо найти только 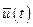 ,
, 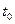 и
и  , так как постоянные интегрирования
, так как постоянные интегрирования 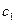 и
и 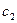 заданы условием (4.19). Таким образом, для нахождения трёх неизвестных
заданы условием (4.19). Таким образом, для нахождения трёх неизвестных 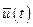 ,
, 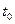 и
и  необходимо решить систему из трёх уравнений. Запишем их.
необходимо решить систему из трёх уравнений. Запишем их.
Оптимальное управление 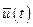 можно определить из уравнения Эйлера (4.14):
можно определить из уравнения Эйлера (4.14):
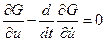 .
.
Для нахождения 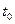 и
и  воспользуемся условиями трансверсальности (4.17) и (4.18), записанными с учётом (4.19) в виде:
воспользуемся условиями трансверсальности (4.17) и (4.18), записанными с учётом (4.19) в виде:
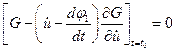 ; (4.20)
; (4.20)
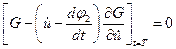 .
.
 2014-02-04
2014-02-04 1023
1023








