Как отмечалось ранее (см. п.4.3), если 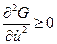 , то функционал
, то функционал  принимает минимальное значение; если
принимает минимальное значение; если 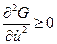 – функционал
– функционал  принимает максимальное значение; если
принимает максимальное значение; если 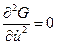 , то экстремаль имеет излом, т.е. является кусочно-гладкой функцией.
, то экстремаль имеет излом, т.е. является кусочно-гладкой функцией.
Найти экстремаль кусочно-гладкой функции, решая уравнение Эйлера, нельзя, так как уравнение Эйлера выводилось в предположении гладкости экстремалей. Поэтому в таком случае поступают следующим образом.
Пусть функционал (4.1) 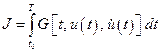 и заданы граничные точки
и заданы граничные точки 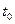 ,
,  ,
,  ,
, 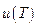 . Предположим, что на отрезке
. Предположим, что на отрезке  в неизвестной точке
в неизвестной точке 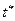 наблюдается единственный излом функции
наблюдается единственный излом функции 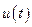 (рис. 4.4).
(рис. 4.4).
 |
Рисунок 4.4 – Экстремаль с изломом
Разобьем отрезок  на два отрезка:
на два отрезка:  и
и 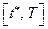 . Тогда функционал
. Тогда функционал  можно представить в виде суммы
можно представить в виде суммы  .
.
Дальнейшее решение задачи аналогично решению задач с подвижными концами (см. (4.14) - (4.18)), но при условии, что эти выражения равны для точек как слева, так и справа излома 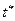 . Запишем уравнение Эйлера и условия трансверсальности для задачи с изломами экстремали:
. Запишем уравнение Эйлера и условия трансверсальности для задачи с изломами экстремали:
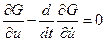 ;
;
 ; (4.21)
; (4.21)
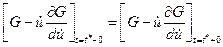 . (4.22)
. (4.22)
Соотношения (4.21) и (4.22) называются условиями Вейерштрасса – Эрдмана. Они используются для нахождения постоянных интегрирования при решении уравнения Эйлера. Для нахождения точки излома 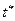 используется условие непрерывности экстремали в этой точке:
используется условие непрерывности экстремали в этой точке: 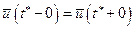 .
.
 2014-02-04
2014-02-04 1162
1162
