Если в вариационных задачах функционал  зависит от нескольких неизвестных функций
зависит от нескольких неизвестных функций 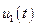 и
и 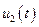 , связанных между собой некоторыми соотношениями (уравнениями связи), то такие задачи называются задачами на условный экстремум.
, связанных между собой некоторыми соотношениями (уравнениями связи), то такие задачи называются задачами на условный экстремум.
Рассмотрим функционал  (4.1), зависящий от
(4.1), зависящий от 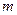 гладких функций
гладких функций 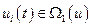 :
:
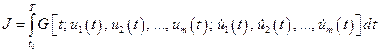 . (4.23)
. (4.23)
Пусть заданы граничные условия 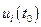 ,
, 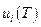 и уравнения связей между переменными.
и уравнения связей между переменными.
Уравнения связей между переменными 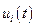 могут быть заданы в одной из трёх форм:
могут быть заданы в одной из трёх форм:
1) алгебраической
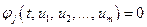 ; (4.24)
; (4.24)
2) дифференциальной
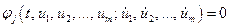 ; (4.25)
; (4.25)
3) интегральной
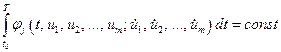 , (4.26)
, (4.26)
где 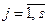 ,
, 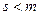 ,
,
 – количество ограничений.
– количество ограничений.
Тогда вариационная задача формулируется следующим образом: в классе гладких функций 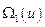 , проходящих через заданные граничные точки функций
, проходящих через заданные граничные точки функций 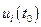 и
и 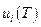 ,
, 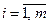 , найти такие функции
, найти такие функции 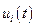 , при которых функционал
, при которых функционал  (4.23) достигает минимума при удовлетворении уравнений связей.
(4.23) достигает минимума при удовлетворении уравнений связей.
Если ограничения (уравнения связи) заданы в алгебраической форме (4.24), то задача называется геодезической, в дифференциальной форме (4.25) – общей задачей Лагранжа, в интегральной форме (4.26) – изопериметрической. Наиболее общей является общая задача Лагранжа, а остальные - могут быть получены как частный случай задачи Лагранжа.
4.8 Метод неопределённых множителей Лагранжа
При решении задач на условный экстремум обычно используют метод неопределённых множителей Лагранжа. В этом случае вместо функционала  (4.23), в котором нет явных связей между переменными, вводится вспомогательный функционал
(4.23), в котором нет явных связей между переменными, вводится вспомогательный функционал 
 , (4.27)
, (4.27)
где 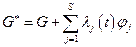 ;
;
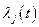 – неопределённые множители Лагранжа;
– неопределённые множители Лагранжа;
 – количество уравнений связи;
– количество уравнений связи;
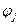 определяются уравнениями (4.24) – (4.26).
определяются уравнениями (4.24) – (4.26).
Далее по методике, изложенной в предыдущих пунктах (см. п.п. 4.2, 4.5), находятся функции 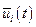 , при которых функционал
, при которых функционал  принимает экстремальное значение. При этом функционал
принимает экстремальное значение. При этом функционал  исследуется на безусловный экстремум.
исследуется на безусловный экстремум.
Аналогично (4.6), уравнение Эйлера записывают в виде:
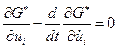 ,
, 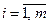 . (4.28)
. (4.28)
С учётом того что 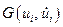 ,
, 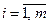 и
и 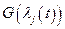 ,
, 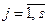 , то имеем замкнутую систему с
, то имеем замкнутую систему с 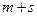 уравнений для нахождения
уравнений для нахождения 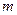 неизвестных функций
неизвестных функций 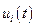 и
и  неизвестных множителей Лагранжа
неизвестных множителей Лагранжа 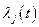 .
.
 2014-02-04
2014-02-04 762
762








