Решение задач оптимального управления вариационными методами

Как отмечалось ранее (см. п.2.2), для описания объекта управления используются уравнения состояния (1.2).

Перепишем уравнение (1.2) в следующей форме:

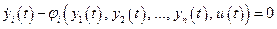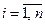, . (4.29)

Пусть заданы начальное и конечное состояния объекта 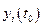и .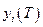

Тогда критерий оптимальности можно записать в следующем виде:

. (4.30)

Необходимо в области допустимых управлений 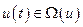найти такое управление 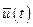, при котором критерий оптимальности достигает наименьшего значения при переходе объекта из заданного начального состояния 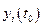в заданное конечное состояние 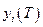по траектории, находящейся в области допустимых состояний .

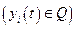В этом случае уравнения объекта (1.2) можно рассматривать как уравнения связей. Из уравнений (1.2) видно, что они заданы в дифференциальной форме, соответствующей (4.25).

Таким образом, для минимизации функционала (4.30) необходимо вначале найти переменные , , …, , .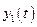

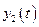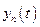Используя метод неопределённых множителей Лагранжа, составляем вспомогательный функционал:

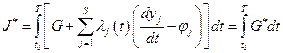. (4.31)

Здесь неизвестным является переменные , , 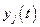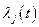при 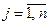. Для их нахождения необходима система 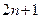уравнений. В качестве такой системы можно использовать 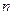уравнений состояния (4.29), 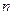уравнений Эйлера для состояний 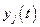(4.28) и равенство нулю первой частной производной 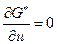, т.е.

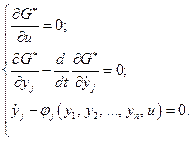
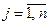(4.32)

С учётом того, что

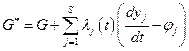(4.33)

систему (4.32) можно записать следующим образом:

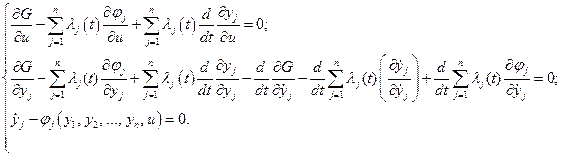(4.34)

В первом уравнении (4.34) третье слагаемое равно нулю, так как 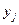не зависит от .

Проанализируем слагаемые во втором уравнении (4.34).

Третье слагаемое равно нулю, так как .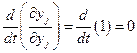

Четвёртое слагаемое равно нулю, так как согласно (4.30) 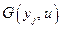и не зависит от .

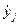Шестое слагаемое равно нулю, так как согласно (4.29) 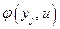и не зависит от .

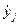С учётом этого система (4.34) примет вид:

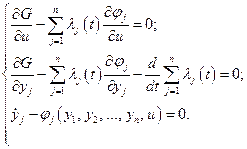
Для установления связи третьего уравнения с неопределёнными множителями Лагранжа найдём частную производную от 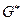(4.33) по .

.

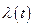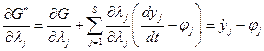В итоге получим следующую систему уравнений:

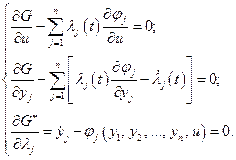(4.35)

Однако не все задачи можно решать с помощью вариационного исчисления. Например, если накладываются ограничения на область допустимых управлений, т.е. 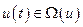(см. (3.1)), то даже если оптимальное управление и не выходит за эту область, а находится на её границе, то это управление 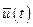нельзя найти, решая уравнение Эйлера, так как мы принимали, что .

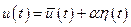Таким образом, методы вариационного исчисления для решения задач оптимального управления можно применять, если функция 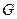в составе функционала является дважды дифференцируемой, а управление 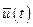и переменные состояния не достигают ограничений.

Если эти условия не выполняются, то для решения задач оптимального управления используются другие специальные методы.