Схема Эйткена
Чаще всего требуется найти не общее выражение Ln(x), а значение его при конкретных x, тогда будет удобно пользоваться интерполяционной схемой Эйткена:
Последовательно вычисляются многочлены:
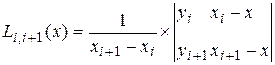
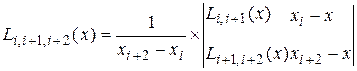
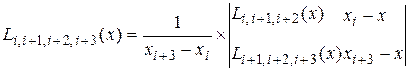
и т.д.
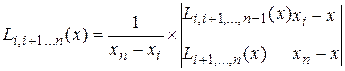
Вычисления по схеме Эйткена удобно расположить в таблице:
| Xi | Yi | Xi-X | Li-1,i | Li-2,i-1,i | Li-3,i-2,i-1,i |
| X0 | Y0 | X0-X | L01 | L012 | L0123 |
| X1 | Y1 | X1-X | L12 | L123 | L1234 |
| X2 | Y2 | X2-X | L23 | L234 | |
| X3 | Y3 | X3-X | L34 | ||
| X4 | Y4 | X4-X |
Вычисления по схеме Эйткена обычно ведутся до тех пор, пока последовательные значения L 01… n(x) и L 01… n(n+ 1 ) не совпадут по заданной точности.
Т.е. процедура является итерационной, легко реализуется и этим обеспечивает возможность автоматического контроля точности вычислений.
Пример: x= 27, 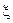 =0,1
=0,1
| i | xi | yi | xi-x | Li-1,i | Li-2,i-1,i | Li-3,i-2,i-1,i | Li-4,i-3,i-2,i-1,i |
| 68,7 | -13 | 48,33 | 49,38 | 49,31 | |||
| 64,0 | -10 | 49,71 | 49,26 | ||||
| 44,0 | 48,90 | 48,21 | |||||
| 39,1 | 50,46 | ||||||
| 32,0 |
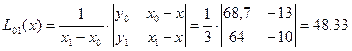
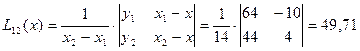
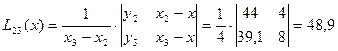
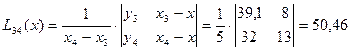
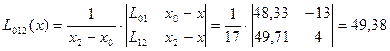
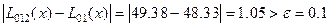
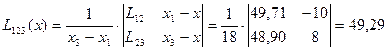

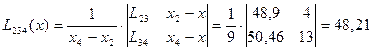
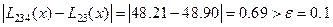
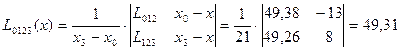
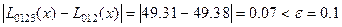
 2014-02-04
2014-02-04 427
427








