Разделённые разности
Если в таблицах встречаются неравноотстоящие значения аргумента, т.е. таблицы с переменным шагом, то вводят понятие разделённых разностей.
Пусть функция 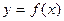 задана таблично, где
задана таблично, где
 - значения аргумента
- значения аргумента
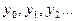 - значения функции
- значения функции
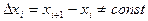
отношения 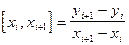 - разделённая разность первого порядка
- разделённая разность первого порядка
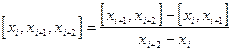 - разделённая разность второго порядка
- разделённая разность второго порядка
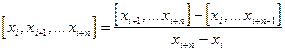 - разделённая разность
- разделённая разность 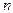 -го порядка
-го порядка
Разделённые разности удобнее всего рассматривать в таблице - таблице разностей
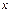
| 
| Разделённые разности | ||||||
| 1-го | 2-го | 3-го | 4-го | |||||
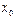
| 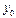
| |||||||
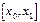
| ||||||||
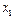
| 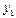
| 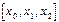
| ||||||
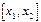
| 
| |||||||
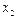
| 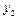
| 
| 
| |||||
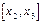
| 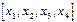
| |||||||
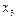
| 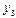
| 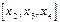
| ||||||
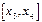
| ||||||||
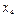
| 
| |||||||
Дано 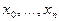 - значения аргумента
- значения аргумента
 - значения функции
- значения функции
Апроксимировать таблично заданную функцию полиномом порядка не выше 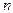
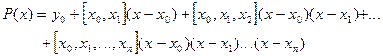
Пример:
| 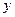
| 1-го | 2-го | 3-го |
| 1,450 | ||||
| 1,127 | ||||
| 1,5 | 3,140 | -0,098 | ||
| 0,795 | - 0,012 | |||
| 3,4 | 4,650 | -0,18 | ||
| -0,159 | ||||
| 6,8 | 4,110 |
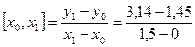
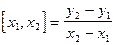
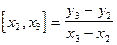
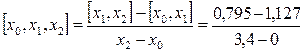
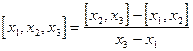
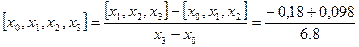
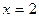
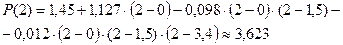
 2014-02-04
2014-02-04 519
519








