Энергетические соотношения в цепи постоянного тока

Теорема об эквивалентном источнике тока (теорема Нортона)

Любой линейный, активный двухполюсник можно заменить эквивалентным источником тока, заданный ток которого равен току короткого замыкания между зажимами двухполюсника и внутренним сопротивлением, которое равно входному сопротивлению пассивного двухполюсника.

Режим короткого замыкания (цепи или генератора) означает работу в ненагруженном режиме, когда выходное напряжение равно нулю, а выходные зажимы закорочены.

Значит, по теореме Нортона, эквивалентны две схемы (рисунок 4.9).

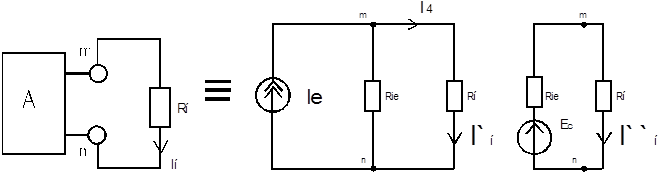
Рисунок 4.10 Графическое пояснение теоремы Нортона

По условиям 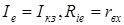согласно с принципа эквивалентности .

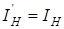Пример 4.3. Для схемы (рисунок 4.7) определим ток 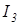, пользуясь теоремой Нортона.

После применения теоремы Нортона получаем следующую схему

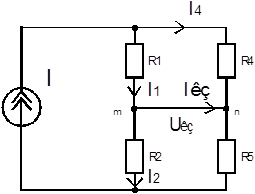
Рисунок 4.11 Схема соединения сопротивлений после преобразовании по теореме Нортона

ток короткого замыкания равен:

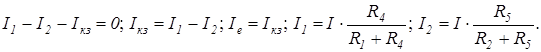
Входное сопротивление пассивного двухполюсника найдено выше, в примере 4.2.

1. По схеме (рисунок 4.12),

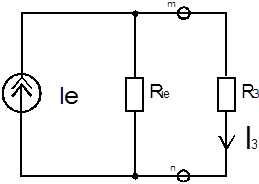
Рисунок 4.12 Схема соединения сопротивлений после преобразований

найдем:

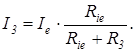
4.6.1.Баланс мощностей.

Алгебраическая сумма мощностей, которые вырабатывают все источники энергии в цепи, равны арифметической сумме мощностей, выделенных на сопротивлениях схемы.

Уравнение баланса мощностей можно представить в таком виде:

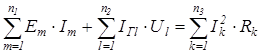(4.1)

где 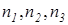– количество источников Э.Д.С., источников тока и резисторов.

Знак направления источника зависит от направления тока через источник Э.Д.С. или напряжения на зажимах источника тока.

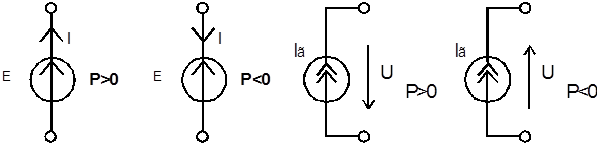
Рисунок 4.13 Обозначение знака направления источников ЭДС и тока

4.6.2 Условие согласования источника с нагрузкой по мощности.

Условие согласования обеспечивает максимальную мощность 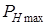, которая потребляется в нагрузке.

Рассмотрим линейный двухполюсник. Заменим его по теореме Тевенена эквивалентным источником напряжения (рисунок 4.6). Выясним, при каком значении сопротивления нагрузки 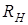мощность 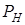, которая в нем теряется, будет максимальной:

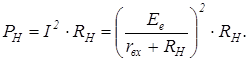
чтобы найти экстремум, решим уравнение:

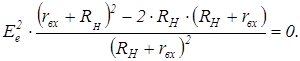
поскольку знаменатель является дополнительной величиной и не может быть равным нулю, приравняем к нулю числитель. Тогда:

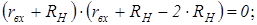
(4.2)

формула (4.2) отвечает требованию согласования. При этом максимальная мощность равна:

.

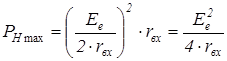При этом мощность, которая вырабатывается источником, будет такой:

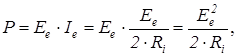
где 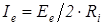– ток нагрузки в режиме согласования.

4.6.2 Понятие коэффициента полезного действия (КПД).

КПД – это отношение полезной мощности к мощности источника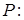

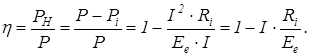
Если 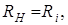значение КПД будет таким: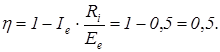

При условии 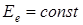, зависимости КПД и мощностей 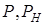от тока в нагрузке изображены на рисунке 4.14, а зависимость 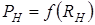– на рисунке 4.15

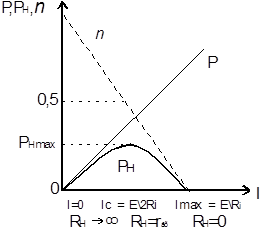
Рисунок 4.14 зависимость КПД и мощностей от тока в нагрузке

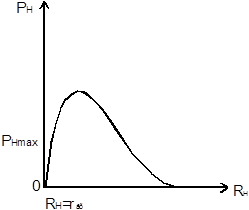
Рисунок 4.15 Зависимость мощности от сопротивления нагрузки

Методические рекомендации.

Для закрепления полученных знаний при изучении подразделов 4.1, 4.2, 4.3 и 4.4 дайте письменные ответы на контрольные вопросы, приведенные ниже.