Теорема об эквивалентном источнике (генератор) используется тогда, когда необходимо найти ток в одной ветви составной цепи. С помощью этой теоремы составная электрическая цепь с приблизительным количеством источников электрической энергии приводится в одноконтурную или двухузловую схему с одним источником, который упрощает расчет цепи. Существует два варианта теоремы.
Теорема об эквивалентном источнике напряжения (теорема Тевенена).
Любой линейный активный двухполюсник можно заменить эквивалентным источником напряжения с ЭДС, которая равна напряжению холостого хода на зажимах двухполюсника, и внутренним сопротивлением, равным выходному сопротивлению пассивного двухполюсника.
Графическое изображение активного и пассивного двухполюсника показано на рисунке 2.1.
Работа в режиме холостого хода (цепи или генератора) означает работу в ненагруженном положении, когда выходной ток равен нулю.
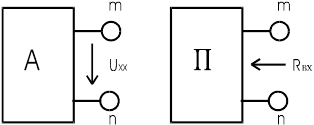
Рисунок 4.5 Графическое изображение двухполюсников в режиме холостого хода
Значит, в соответствии с теоремой возможна эквивалентная замена (рисунок 4.5) причем, 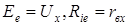 .
.
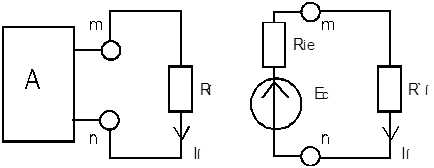
Рисунок 4.6 Принцип последовательности преобразований схемы двухполюсника по теореме Тевенена
По принципу эквивалентности внешние токи (напряжения) не изменяются: ток в нагрузке одинаков для обеих схем 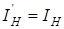 :
:
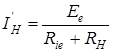
Пример 4.2. По теореме Тевенена, обозначим ток в сопротивлении 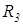 (рисунок 4.7).
(рисунок 4.7).
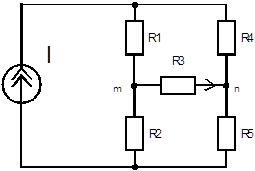
Рисунок 4.7 Схема соединения сопротивлений
1. Заменим активный двухполюсник относительно узлов 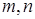 эквивалентным источником напряжения с параметрами
эквивалентным источником напряжения с параметрами 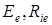 (рисунок 4.8).
(рисунок 4.8).
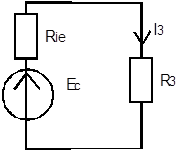
Рисунок 4.8 Схема соединения сопротивлений после замены источника тока источником напряжения
2. Определим значение ЭДС 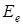 , как напряжение холостого хода при размыкании
, как напряжение холостого хода при размыкании 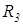 для схемы (рисунок 4.9):
для схемы (рисунок 4.9):
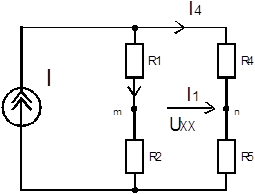
Рисунок 4.9 схема соединений сопротивлений при размыкании R3
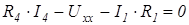 ;
; 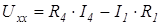 ;
;
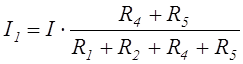 ;
; 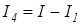
3. Рассчитаем входное сопротивление пассивного двухполюсника со стороны узлов m, n (предположим, что для перехода от активного к пассивному двухполюснику необходимо источник идеального Э.Д.С. разомкнуть, а идеальный источник тока замкнуть):
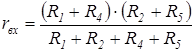 ;
; 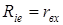
4. Рассчитаем искомый ток I3 по закону Ома по схеме (рисунок 4.8):
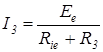
 2014-02-04
2014-02-04 1135
1135
