Два метода изучения движения жидкости

И УРАВНЕНИЯ КИНЕМАТИКИ

ОСНОВНЫЕ ПОНЯТИЯ, ОПРЕДЕЛЕНИЯ

ГИДРОСТАТИКА.

Существует два метода изучения движения жидкости: метод Лагранжа и метод Эйлера.

В методе Лагранжа наблюдают за движением каждой отдельной частицы жидкости, исследуя её траекторию. Координаты X₀, Y₀, Z₀, соответствующие начальному моменту времени t = t₀, присва­иваются частице как наименование, позволяющее в любой момент времени отличить её от других частиц.

Положение любой частицы в процессе движения, определяемое значением её радиуса – вектора или декартовых координат X, Y, Z, будет функцией её начальных координат (X₀, Y₀, Z₀) и времени (t):

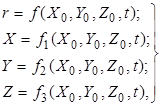(3.1)

где X₀, Y₀, Z₀ называют переменными Лагранжа.

Чтобы получить скорость определенной частицы и её проекции на координатные оси, следует продифференцировать уравнения (3.1) по времени (t), считая начальные координаты X₀, Y₀, Z₀ постоянными:

(3.2)

Величину ускорения определенной частицы и ее проекции на координатные оси получим, продифференцировав уравнение (3.2) по времени, по-прежнему считая начальные координаты постоянными.

Производная во времени, вычисляемая в переменных Лагранжа, получила название индивидуальной или субстанциональной (поскольку она относится к определенной частице субстанции).

Метод Лагранжа, дающий весьма подробное описание поведения движущейся частицы, не получил, однако, широкого распространения из-за своей громоздкости и сложности:

(3.3)

Для решения большинства практических задач представляет интерес не столько поведение индивидуальной частицы, сколько со­стояние движения в каждый момент времени в каждой точке пространства.

Такое описание движения жидкости проводится при помощи метода Эйлера. В этом методе внимание наблюдателя сосредоточива­ется не на той или иной частице, а на определенной точке пространства, занятого движущейся жидкостью, и исследуется зависимость скорости различных частиц, непрерывно следующих одна за другой через эту точку от координат этой точки X, Y, Z и от времени t:

,

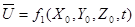или в проекциях на оси координат:

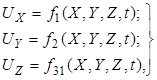(3.4)

где X, Y, Z − называют переменными Эйлера.

Величины X, Y, Z имеют в методах Лагранжа и Эйлера различный смысл. В первом методе эти величины представляют переменные координаты одной и той же движущейся жидкости, во втором являются постоянными координатами одних и тех же точек пространства, через которые в разные моменты времени проходят различные частицы жидкости.

Если в уравнениях (3.4) считать t постоянным, а X, Y, Z переменными, то получим распределение скоростей частиц жид­кости в пространстве для определенного момента времени.

При постоянных значениях X, Y, Z и переменном t получим зависимость скорости жидкости от времени для данной точки пространства, причем в разные моменты времени определяемые значения скорости будут относиться к различным частицам жидкости.

В том случае, когда желательно выяснить, каким образом изменяется скорость с течением времени в данной точке (X, Y, Z) пространства, следует продифференцировать уравнения по време­ни, считая координаты X, Y, Z величинами постоянными.

Если же нас интересует вопрос о том, какое ускорение испытывает определенная частица, проходящая в данный момент времени через точку (X, Y, Z) пространства, то следует рассматривать координаты X, Y, Z как величины переменные, зависящие от времени, ибо за тот бесконечно малый промежуток времени dt,в течение которого ведется наблюдение за изменением скорости частицы, она успевает перейти из точки (X, Y, Z) в другое положение.

Таким образом, скорость частицы зависит от времени как непосредственно, так и через посредство координат X, Y, Z в свою очередь являющихся функциями времени. Поэтому ускорение частицы следует вычислить, пользуясь уравнением (3.4) по правилу дифференцирования сложной функции:

. (3.5)

Так как

,

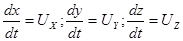имеем

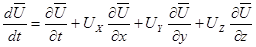. (3.6)

Аналогично для компонентов ускорения частицы

(3.7)

Первый член правой части уравнения (3.7) 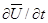выражает локальное (местное) ускорение частицы. Он характеризует изменение скорости во времени в данной точке пространства, обусловленное нестационарностью скоростного поля. Последующие три члена представляют изменения скорости частицы, обусловленные изменением её координат, и называются конвективными ускорениями.

Вынося из уравнений (3.6) символически за скобку вектор скорости 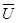, получим

.

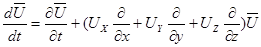Выражение в скобках может быть представлено как скалярное произведение вектора скорости:

,

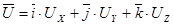на символический вектор 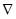(дифференциальный оператор набла):

,

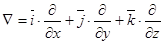и записано в виде

.

Аналогичные преобразования могут быть проведены и в осталь­ных уравнениях (3.7) для компонентов ускорения по координатным осям (X, Y, Z). После этого можно переписать уравнения (3.6) и (3.7) в виде

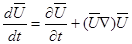; (3.8)

(3.9)