Таблица 2.5.
Значение коэффициентов x некоторых местных сопротивлений
Номограмма Кольбрука-Уайта для определения коэффициента гидравлического трения

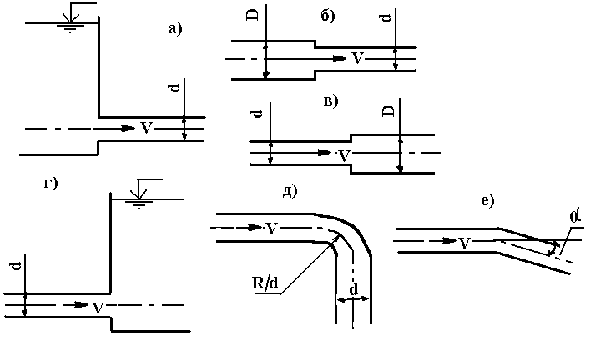
| Тип препятствия | Схема сопротивл. по рисунку | Значение коэффициентов x |
| Вход в трубу Внезапное сужение Внезапное расширение Выход из трубы | а б в г | 0,50 0,50 [1 - (d / D)2] [(D / d)2 - 1]2 1,0 |
Таблица 2.6.
| Плавный поворот (см. схему на рис. д) | Крутой поворот (см. схему на рис. е) | ||
| d / D | x | a ° | x |
| 0,20 0,40 0,60 0,80 — | 0,14 0,21 0,44 0,98 — | 0,12 0,16 0,32 0,56 1,19 |
Контрольные задания, выполняемые студентами, преследуют двоякую цель: с одной стороны, более глубоко изучить основные положения курса гидравлики, а с другой стороны – применить изученные закономерности при решении практических задач.
Задачи 1, 2, 3. Эти задачи составлены по теме «Основные свойства жидкостей». В задаче 1 рассматриваются сжимаемость и температурное расширение, а в задачах 2, 3 – вязкость жидкости.
При решении задачи 1 используют известные формулы для определения коэффициентов объемного сжатия и температурного расширения жидкости. Интересно, что повышение давления в герметичном, заполненном жидкостью сосуде не зависит от его объема.
Задачу 2 решают с помощью формулы Ньютона:
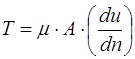 ,
,
где Т – сила трения; m – динамическая вязкость жидкости; А – площадь соприкосновения твердой поверхности с жидкостью; du/dn – градиент скорости. Поскольку толщина слоя масла мала, можно считать, что скорости в нем изменяются по прямолинейному закону. Следовательно, градиент скорости du/dn = υ/d. Пластина скользит под воздействием силы 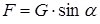 , где G – сила тяжести пластины. При равномерном движении пластины сила трения Т по величине равна силе F.
, где G – сила тяжести пластины. При равномерном движении пластины сила трения Т по величине равна силе F.
Задачу 3 решают по той же методике, что и задачу 2, только силу трения в данном случае определяют из формулы момента
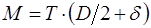 .
.
Из-за малости зазора вторым членом d в скобках можно пренебречь. При малом зазоре, когда d << D, кривизной слоя жидкости пренебрегают, рассматривая её движение в зазоре как плоскопараллельное (см. рис. 2.2, б). Считая, что скорости U в слое масла изменяются по прямолинейному закону, эпюра касательных напряжений τ имеет вид прямоугольника. Следовательно, сила трения Т проходит через центр тяжести этой эпюры, т.е. по середине слоя масла. Угловую скорость w и частоту n вращения вала определяют при помощи известных формул:
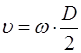 ,
, 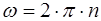 .
.
Задачи 4, 5, 6. Эти задачи составлены по теме «Гидростатика». Они связаны с определением силы давления жидкости на криволинейные стенки.
При решении задачи 4 определяют горизонтальную 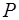 x и вертикальную P z составляющие равнодействующей силы давления жидкости.
x и вертикальную P z составляющие равнодействующей силы давления жидкости.
Задачи 7, 8, 9. Эти задачи рассматривают относительный покой жидкости.
Задачи 10, 11, 12. Эти задачи составлены по теме «Гидравлический расчет трубопроводов» к разделу гидравлически коротких трубопроводов. Их решают с помощью уравнения Бернулли. При этом учитывают как потери по длине, так и местные потери.
Ход решения задач следующий:
1) выбирают два живых сечения в потоке так, чтобы в них было известно наибольшее число входящих в уравнение Бернулли гидродинамических параметров (z, р, v). За первое сечение можно брать свободную поверхность жидкости в резервуаре А (задачи 10 и 12), свободную поверхность в колодце (задача 11); за второе сечение – свободную поверхность в канале Б (задача 11), место подключения вакуумметра (задача 12) или место подключения манометра (задача 13);
2) намечают горизонтальную плоскость сравнения, проходящую через центр тяжести одного из расчетных сечений;
3) для выбранных сечений выписывают уравнение Бернулли и определяют отдельные его слагаемые:
– геометрические высоты z 1 и z 2 выше плоскости сравнения считаются положительными, а ниже – отрицательными;
– давление на поверхности открытых резервуаров равно атмосферному, а в закрытых резервуарах или в трубе – сумме атмосферного давления и давления, снятого на приборе (манометрическое давление со знаком плюс, вакуумное – со знаком минус);
– скоростной напор 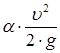 в резервуарах является ничтожным по сравнению с другими членами уравнения Бернулли и приравнивается нулю;
в резервуарах является ничтожным по сравнению с другими членами уравнения Бернулли и приравнивается нулю;
– гидравлические потери состоят из потерь по длине и местных потерь;
4) преобразуют уравнение Бернулли, с тем, чтобы определить оставшееся неизвестное.
Задачи 10 и 12 рекомендуется решать графоаналитическим путем при помощи кривой взаимозависимости между высотой напора Н и диаметром d трубопровода: H = ¦(d). По выбранным значениям диаметра трубопровода d определяют коэффициент гидравлического трения l и высоту напора Н. По полученным данным и строят кривую Н = ¦(d). При помощи кривой по известному напору Н определяют диаметр d.
Для построения пьезометрической и напорной линий выбирают вспомогательные вертикали по концам труб одинакового диаметра или осям местных сопротивлений. Проводят линию первоначальной энергии (напора), вниз на каждой последующей вертикали откладывают гидравлические потери, рассчитанные между этими вертикалями. Через полученные точки проводят линию, которая является напорной линией. Если на каждой вертикали вниз от ранее отмеченных точек откладывать значения кинетических энергий 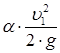 ,
, 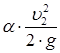 , и т.д., получим пьезомет-рическую линию. Она параллельна напорной линии и находится ниже её.
, и т.д., получим пьезомет-рическую линию. Она параллельна напорной линии и находится ниже её.
Задачи 10 и 12 можно решать на ЭВМ.
Задачи 13, 14, 15. Эти задачи составлены по той же теме, что и задачи 10, 11, 12, но относятся к разделу гидравлически длинных и сложных трубопроводов. Их также решают с помощью уравнения Бернулли, но учитывают лишь потери по длине, а местные потери принимают равными некоторой доле потерь по длине. Методика решения задач имеет сходство с решением задачи 10. Гидравлические потери определяют графоаналитически, составляя гидравлическую характеристику трубопровода Н = ¦(Q). Прежде всего, строят характеристики отдельных простых трубопроводов по данным расчета потерь напора при различных значениях расхода. На основе характеристик отдельных трубопроводов строят общую характеристику трубопровода.
При расчете последовательно соединенных труб общую характеристику трубопровода получают путем сложения гидравлических характеристик отдельных труб по направлению оси напора Н, так как по всем участкам такого трубопровода протекает одинаковый расход (задача 13), т.е. потери всего трубопровода равны сумме потерь отдельных труб.
В случае параллельно соединенных трубопроводов (задача 14) общую гидравлическую характеристику трубопровода получают путем сложения отдельных характеристик по направлению оси расхода Q, так как гидравлические потери во всех параллельных линиях являются равными.
При смешанном соединении труб (задача 15) вначале складывают гидравлические характеристики параллельно соединенных труб (по оси Q), а потом к ним добавляют гидравлическую характеристику последовательно присоединенной трубы (по оси H). При помощи кривой Н = ¦(Q) по известному напору Н определяют расход Q.
Задачи 13, 14, 15 можно решать на ЭВМ.
Задачи 16, 17, 18. Эти задачи составлены по теме «Истечение жидкости через отверстия и насадки». При их решении применяют формулу расхода жидкости при ее истечении через отверстие или насадок, а действующий напор определяют по формуле. В случае затопленного отверстия или насадка за действующий напор берется разница пьезометрических напоров по обе стороны стенки. Можно считать, что коэффициент расхода m не зависит от числа Рейнольдса, т.е. является постоянным: для отверстия m = 0,62, для цилиндрического насадка m = 0,80, для коноидального насадка m = 0,97.
 2014-02-05
2014-02-05 2547
2547







