Дано: 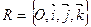 ,,
,,
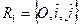 , g: F (x; y)=0 (в плоскости хОу).
, g: F (x; y)=0 (в плоскости хОу).
Доказать: S: F (x; y)=0.
Доказательство.
самостоятельно
Определение 5.
Цилиндр называется круговым, эллиптическим, параболическим, гиперболическим в зависимости от вида направляющей его линии – окружности, эллипса, параболы, гиперболы.
Цилиндр называется прямым, если его образующая параллельна координатной оси, а направляющая линия лежит в плоскости, параллельной координатной плоскости (перпендикулярной к образующей).
Примеры:
| Название | Уравнение
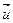 || Оz (или || Оz (или 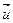 || || 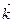 ) )
| Уравнение
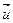 || Ох
(или || Ох
(или 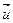 || || 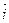 ) )
| Уравнение
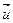 || Оу
(или || Оу
(или 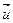 || || 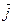 ) )
|
| Эллиптический цилиндр | 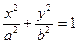
| 
| 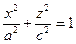
|
| Прямой круговой цилиндр (цилиндр вращения) | 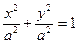 или
или 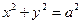
| ||
| Гиперболический цилиндр | 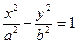
| ||
| Параболический цилиндр | 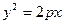
| ||
Пара пересекающихся плоскостей,
пересечение – образующая прямая l ||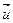 (ось) (ось)
|  ,
или ,
или 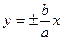 ,
пересечение – прямая Оz ,
пересечение – прямая Оz
| ||
Пара параллельных плоскостей,
симметричных относительно оси с направляющим вектором 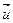 и удаленных от нее на расстояние а и удаленных от нее на расстояние а
| 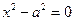 или
или 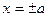
| ||
| Пара совпадающих плоскостей | 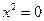 или
или 
|
 2014-02-05
2014-02-05 263
263








