ЛЕКЦИЯ № 12
Контрольные вопросы
Begin
a.re:= 1; a.im:= 1;
b.re:= 1; b.im:= 2;
AddC(a, b, c);
WriteLn('Сложение: 'c.re:5:1, c.im:5:1,'i');
SubC(a, b, c);
WriteLn('Вычитание: 'с.re:5:1, с.im:5:1,'i');
MulC(a, b, c);
WriteLn('Умножение: 'c.re:5:1, c.im:5:l,'i');
DivC(a, b, c);
WriteLn('Деление: 'c.re:5:l, с.im:5:1,'i');
end.
После объявления Uses Cmplx программе стали доступны все объекты, объявленные в интерфейсной части модуля CMPLX. При необходимости можно переопределить любой их этих объектов, как это произошло, например, с объявленной в модуле типизированной константой С. Переопределение объекта означает, что вновь объявленный объект «закрывает» ранее определенный в модуле одноименный объект. Чтобы получить доступ к «закрытому» объекту, нужно воспользоваться составным именем: перед именем объекта поставить имя модуля и точку. Например, оператор
WriteLn(cmplx.c.re:5:l, cmplx.с.im:5:1,'i'); выведет на экран содержимое «закрытой» типизированной константы из предыдущего примера.
1 Стандартные модули в Паскале.
2 Структура модуля.
3 Ключевые слова Unit, Interface, Implementation. Описание каждого раздела.
4 Концепция разработки собственного модуля. Примеры программ.
Один из наиболее часто встречающихся случаев несимметричного режима трехфазной цепи получается при соединении фаз несимметричного приемника по схеме звезда без нейтрального провода или с нейтральным проводом, комплексное сопротивление которого 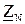 необходимо учитывать при расчете.
необходимо учитывать при расчете.
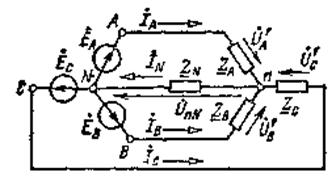
Рисунок 1
При заданном действующем значении линейного напряжения приемника 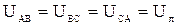 можно дополнить трехфазную цепь воображаемым симметричным трехфазным источником ЭДС, соединенным по схеме звезда (рисунок 1), с действующим значением фазной ЭДС:
можно дополнить трехфазную цепь воображаемым симметричным трехфазным источником ЭДС, соединенным по схеме звезда (рисунок 1), с действующим значением фазной ЭДС: 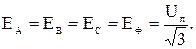
Полученная цепь имеет две нейтральные точки: симметричного генератора N и несимметричного приемника n – два узла цепи. Поэтому для расчета режима цепи следует применить метод двух узлов, заменив в проводимости ветвей цепи постоянного тока 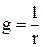 комплексными проводимостями ветвей цепи синусоидального тока
комплексными проводимостями ветвей цепи синусоидального тока 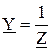 , а постоянные ЭДС и токи – комплексными значениями соответствующих синусоидальных ЭДС и токов. В рассчитываемой трехфазной системе комплексное значение напряжения
, а постоянные ЭДС и токи – комплексными значениями соответствующих синусоидальных ЭДС и токов. В рассчитываемой трехфазной системе комплексное значение напряжения 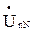 между нейтральными точками приемника n и воображаемого генератора N называется напряжением смещения нейтрали. На основании метода двух узлов
между нейтральными точками приемника n и воображаемого генератора N называется напряжением смещения нейтрали. На основании метода двух узлов
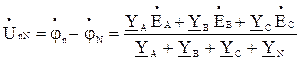 (1)
(1)
или с учетом 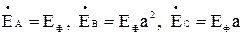 и равенства
и равенства 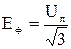 комплексное значение напряжения смещения нейтрали
комплексное значение напряжения смещения нейтрали
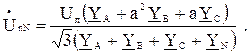 (2)
(2)
Фазные напряжения приемника определяются по второму закону Кирхгофа для трех контуров:
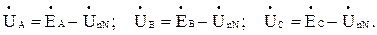 (3)
(3)
По закону Ома фазные токи и ток в нейтральном проводе соответственно равны:
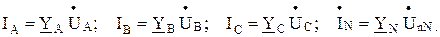 (4)
(4)
Распределение напряжений между фазами несимметричного приемника, которые соединены по схеме звезда, наглядно иллюстрирует потенциальная диаграмма цепи (рисунок 2, а).
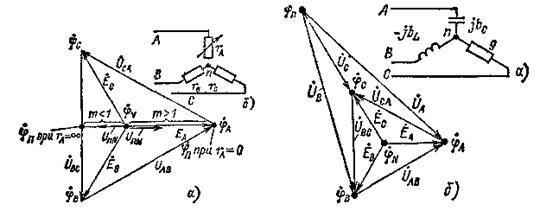
Рисунок 2 Рисунок 3
При построении потенциальной диаграммы равный нулю потенциал выбран у нейтральной точки N воображаемого генератора, которая служит началом отсчета. Из начала отсчета построены три вектора фазных ЭДС воображаемого генератора 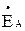 ,
, 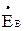 и
и 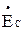 . Концы этих векторов определяют комплексные значения потенциалов
. Концы этих векторов определяют комплексные значения потенциалов 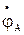 ,
, 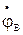 и
и 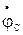 линейных проводов А, В и С при
линейных проводов А, В и С при 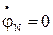 , а следовательно линейных напряжений
, а следовательно линейных напряжений 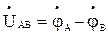 ,
, 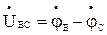 ,
, 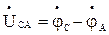 . При симметричном приемнике нет смещения нейтрали, т. е.
. При симметричном приемнике нет смещения нейтрали, т. е. 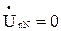 , и потенциал нейтральной точки приемника
, и потенциал нейтральной точки приемника 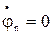 . Поэтому на диаграмме потенциал нейтральной точки приемника
. Поэтому на диаграмме потенциал нейтральной точки приемника 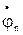 совпадает с нейтральной точкой генератора
совпадает с нейтральной точкой генератора 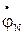 . При несимметричном приемнике смещение нейтрали
. При несимметричном приемнике смещение нейтрали 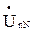 , как следует из (1), не равно нулю. Поэтому потенциал нейтральной точки приемника
, как следует из (1), не равно нулю. Поэтому потенциал нейтральной точки приемника 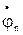 смещается относительно потенциала нейтральной точки генератора
смещается относительно потенциала нейтральной точки генератора 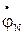 , т. е. из центра треугольника линейных напряжений (смещение нейтрали).
, т. е. из центра треугольника линейных напряжений (смещение нейтрали).
Рассмотрим простейший случай приемника с активными сопротивлениями фаз 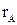 и
и 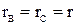 при отсутствии нейтрального провода (рисунок 2, б). Проводимости фаз В и С одинаковые:
при отсутствии нейтрального провода (рисунок 2, б). Проводимости фаз В и С одинаковые: 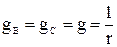 , а проводимость
, а проводимость 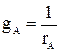 фазы А изменяется от 0 до ∞. Обозначим отношение
фазы А изменяется от 0 до ∞. Обозначим отношение 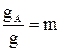 и найдем напряжение смещения нейтрали по (1), учитывая (
и найдем напряжение смещения нейтрали по (1), учитывая (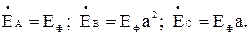 ):
):
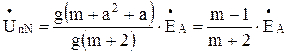
или
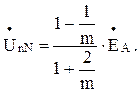
При изменениях проводимости 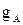 в пределах от нуля до бесконечности множитель при ЭДС
в пределах от нуля до бесконечности множитель при ЭДС 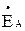 остается действительной величиной. Следовательно, напряжение смещения нейтрали
остается действительной величиной. Следовательно, напряжение смещения нейтрали 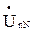 совпадает по фазе с ЭДС
совпадает по фазе с ЭДС 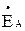 при
при 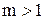 , а при
, а при 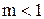 их фазы отличаются на
их фазы отличаются на 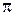 (рисунок 2, а). В частности, при размыкании фазы А, т. е.
(рисунок 2, а). В частности, при размыкании фазы А, т. е. 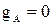 или
или 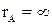 и
и 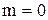 , смещение нейтрали
, смещение нейтрали
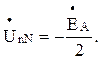
При этом фазные напряжения приемника равны:
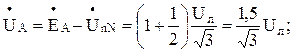
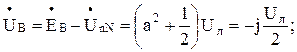
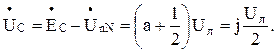
Здесь учтено, что 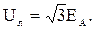
При 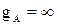 или
или  , т. е. коротком замыкании точек А и n (рисунок 2, б), очевидно, что будет
, т. е. коротком замыкании точек А и n (рисунок 2, б), очевидно, что будет  ;
; 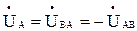 ;
; 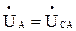 .
.
Потенциал нейтральной точки приемника может сместиться далеко за пределы треугольника линейных напряжений, если проводимости фаз приемника, соединенных по схеме звезда без нейтрального провода, различны по характеру.
Рассчитаем, например, смещение нейтрали и фазные напряжения для приемника с комплексными проводимостями фаз 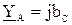 ,
, 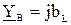 ,
,  при условии
при условии 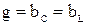 (рисунок 3, а).
(рисунок 3, а).
Смещение нейтрали по (1)
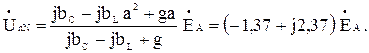 (5)
(5)
Фазные напряжения приемника рассчитываются так же, как и для приемника по рисунку 2, б. Для действующих значений напряжений в результате расчета получается:
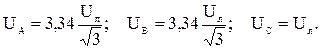
Потенциальная диаграмма показана на рисунке 3, б.
Схема цепи по рисунку 3, а имеет важное свойство, которое используется в различных устройствах. Если емкостная проводимость фазы А и индуктивная проводимость фазы В одинаковые и постоянные: 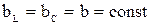 , то ток в фазе С не зависит от значения активной проводимости
, то ток в фазе С не зависит от значения активной проводимости 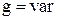 этой фазы. Действительно из векторной диаграммы на рисунок 3, б и формулы (5) следует, что
этой фазы. Действительно из векторной диаграммы на рисунок 3, б и формулы (5) следует, что
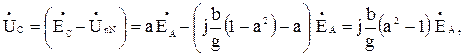
т. е.
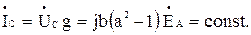
Фазные токи несимметричного приемника, фазы которого соединены по схеме треугольник (рисунок 4), при заданных линейных напряжениях определяются по закону Ома:
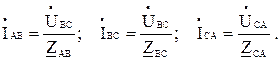
Линейные токи рассчитываются на основании первого закона Кирхгофа:
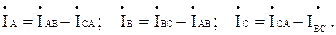
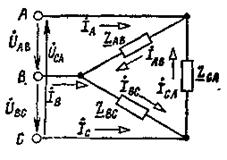
Рисунок 4
При расчете более сложной несимметричной трехфазной цепи, с несимметричными приемниками все приемники путем преобразований заменяются эквивалентным, фазы которого соединены по схеме звезда. Эти преобразования выполняются в той же последовательности, что и для симметричных приемников, но сопротивление каждой фазы эквивалентного приемника приходится вычислять отдельно.
 2014-02-05
2014-02-05 1057
1057







