Комплексный чертеж точки

Теорема о проецировании прямого угла.

Если один из катетов прямого угла параллелен плоскости проекций, а второй не занимает проецирующего положения (не перпендикулярен плоскости проекций), то данный прямой угол на эту плоскость проекций проецируется без искажения.

Вышеприведенные чертежи называются однокартинными. Рассмотренные методы проецирования позволяют однозначно решить прямую задачу – построить проекцию (чертеж) геометрического образа.

Обратная задача начертательной геометрии – по данному чертежу реконструировать геометрический образ – решается неоднозначно (может быть несколько или бесчисленное множество решений). Из этого следует, что однокартинный чертеж не обладает свойством обратимости. Проекционный чертеж становится обратимым при добавлении дополнительной информации.

В нашем курсе мы будем применять обратимый чертеж, который называется комплексным чертежом в ортогональных проекциях (К.Ч.)

Комплексным чертежом называется чертеж, составленный из двух или более связанных между собой ортогональных проекций изображаемого геометрического образа.

Принцип образования: геометрический образ ортогонально проецируется минимум на две взаимно перпендикулярные плоскости проекций, которые затем соответствующим образом совмещаются с одной плоскостью.

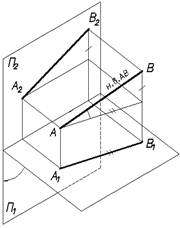Точка - нольмерный геометрический образ;

Условные обозначения точек – A,В,С,D… 1,2,3… и т.д.;

П 1 (XOY) – горизонтальная плоскость

проекции;

П 2 (XOZ) – вертикальная (фронтальная) плоскость проекции;

А 1 – горизонтальная проекция точки А на плоскость П1;

А 2 – фронтальная проекция точки А на плоскость П 2.

Рис.6 Чертеж на рис.6 является однокартинным.

Чертеж на рис. 7 называется комплексным чертежем точки А.

А 1 – горизонтальная проекция точки А;

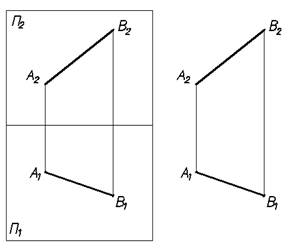А 2 – фронтальная проекция точки А;

А 1 А 2- линия связи.

Оба чертежа (рис.6 и рис.7) являются графической иллюстрацией ортогонального проецирования одной и той же точки А на две взаимно перпендикулярные плоскости (П 1 и П 2).

Если на К.Ч. заданы две проекции точки, можно утверждать, что точка однозначно задана на К.Ч.

Рис.7