Винтовые поверхности. Винтовыминазываются поверхности, получаемые при винтовом движении образующей

Винтовыми называются поверхности, получаемые при винтовом движении образующей.

Рассмотрим винтовые поверхности, у которых образующая – прямая линия.

Такие поверхности называются линейчатыми винтовыми поверхностями или геликоидами.

Прямой геликоид U (n, i, П 1)(Рис.28)

(n, i, П 1) – определитель поверхности

Состав определителя:

n – цилиндрическая винтовая линия;

i – ось цилиндрической винтовой линии; П 1 – плоскость параллелизма.

(i ^ П 1 – обязательное условие);

Закон образования поверхности

(закон Каркаса):

Рис.28 l x n; l х i;

l II П 1.

Прямой геликоид одновременно является и винтовым коноидом.

Наклонный геликоид W (n, i, Г) (Рис.29)

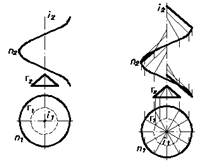(n, i, Г) –определитель поверхности.

Состав определителя:

n – цилиндрическая винтовая линия;

i – ось данной винтовой линии;

Г – направляющий конус.

Ось направляющего конуса Г совпадает с осью i (обязательное условие).

Закон образования поверхности

(закон Каркаса):

Рис.29 l i x n; l iх i; l i II Г.

Образующая наклонного геликоида, пересекая n и i во всех своих положениях, остается параллельной соответствующей образующей наклонного геликоида (обе образующие и ось i находятся в одной плоскости). Также можно сказать, что образующая наклонного геликоида пересекает ось i под постоянным углом, равным половине угла при вершине направляющего конуса.