Пусть прямая L проходит через точку 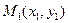 и образует с положительным направлением оси Ох угол α (
и образует с положительным направлением оси Ох угол α (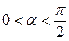 ).
).
Возьмем на прямой  точку
точку 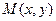 .
.
Очевидно, 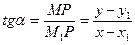 . (4.1)
. (4.1)
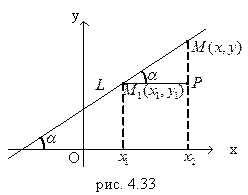
Обозначим 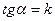 и назовем угловым коэффициентом прямой L.
и назовем угловым коэффициентом прямой L.
Из (4.1) получаем:
y-y 1 =k (x-x 1) (4.2)
Можно показать, что уравнение (4.2) справедливо и для случая 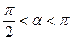 .
.
Уравнение (4.2) называется уравнением прямой, проходящей через данную точку в данном направлении.
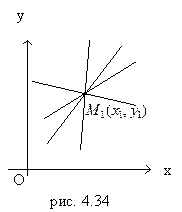
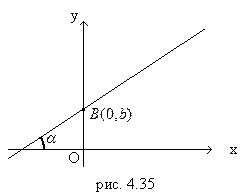 Если в уравнении (4.2) k – произвольное число, то уравнение (4.2) определяет пучок всевозможных прямых (кроме вертикальной прямой), где точка
Если в уравнении (4.2) k – произвольное число, то уравнение (4.2) определяет пучок всевозможных прямых (кроме вертикальной прямой), где точка 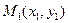 - центр пучка (рис. 4.34).
- центр пучка (рис. 4.34).
Пусть известно, что прямая, имеющая угловой коэффициент  , отсекает на оси Оу отрезок, равный b, то есть проходит через точку B (0, b).
, отсекает на оси Оу отрезок, равный b, то есть проходит через точку B (0, b).
Используя уравнение (4.2) получаем уравнение:
y=kx+b, (4.3)
которое называется уравнением прямой с угловым коэффициентом.
Поведение прямой определяется параметрами k и b.
1. 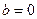 ,
, 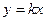 , прямая проходит через начало координат.
, прямая проходит через начало координат.
2. 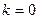 ,
, 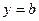 , прямая параллельна оси Ох.
, прямая параллельна оси Ох.
3. 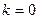 ,
, 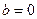 ,
,  - уравнение оси Ох. (рис. 4.36)
- уравнение оси Ох. (рис. 4.36)
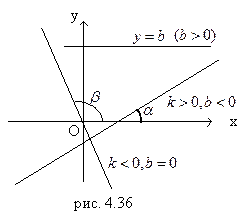

Пусть даны две точки 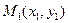 и
и 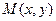 , через которые проходит прямая и
, через которые проходит прямая и 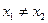 ,
, 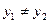 (рис. 4.37). Угловой коэффициент этой прямой
(рис. 4.37). Угловой коэффициент этой прямой 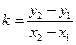 . Подставим его в уравнение (4.2) и получим:
. Подставим его в уравнение (4.2) и получим:
|
|
|
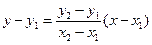 или
или
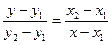 . (4.4)
. (4.4)
Получено уравнение прямой, проходящей через две данные точки.
 Пусть прямая параллельна оси Оу и отсекает от оси Ох отрезок, равный а. Очевидно, для любой точки М, принадлежащей прямой L, абсцисса:
Пусть прямая параллельна оси Оу и отсекает от оси Ох отрезок, равный а. Очевидно, для любой точки М, принадлежащей прямой L, абсцисса:
х=а (4.5)
Получено уравнение вертикальной прямой.
Уравнения (4.2)-(4.5) показывают, что любая прямая описывается линейным уравнением (линейной функцией).
Покажем, что всякое линейное уравнение
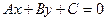 (4.6)
(4.6)
определяет прямую на плоскости, если А и В одновременно не обращаются в ноль.
1. Пусть 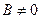 , тогда
, тогда 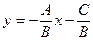 . Обозначим
. Обозначим 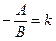 ,
, 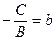 . Тогда уравнение (4.6) принимает вид
. Тогда уравнение (4.6) принимает вид 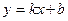 , то есть определяет прямую.
, то есть определяет прямую.
2. 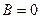 ,
, 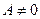 , получаем
, получаем 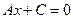 , или
, или 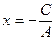 . Обозначим
. Обозначим 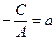 . Получим уравнение
. Получим уравнение 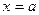 , но это уравнение определяет вертикальную прямую (4.5).
, но это уравнение определяет вертикальную прямую (4.5).
3. 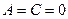 , тогда
, тогда 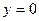 - уравнение оси Ох;
- уравнение оси Ох;
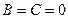 , тогда
, тогда 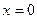 - уравнение оси Оу.
- уравнение оси Оу.
Таким образом, при любых значениях коэффициентов А и В и свободного члена С уравнение (4.6) определяет прямую линию на плоскости хОу. Оно называется общим уравнением прямой на плоскости.
Угол между прямыми. Условия параллельности и перпендикулярности прямых.
 Пусть известны угловые коэффициенты прямых L 1 и L 2, равных k 1 и k 2 соответственно,
Пусть известны угловые коэффициенты прямых L 1 и L 2, равных k 1 и k 2 соответственно, 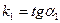 ,
, 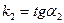 (рис. 4.39).
(рис. 4.39).
 Угол между прямыми
Угол между прямыми 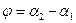 , при этом
, при этом  ,
, 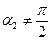 .
.
Тогда 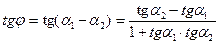 , откуда получаем
, откуда получаем 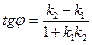 ,где стрелка означает, что угол
,где стрелка означает, что угол 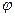 получается при повороте прямой L 1 к прямой L 2 против часовой стрелки.
получается при повороте прямой L 1 к прямой L 2 против часовой стрелки.
Если прямые параллельны, то есть 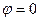 , то
, то 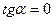 , следовательно k 1= k 2 - условие параллельности прямых. Если прямые перпендикулярны, то
, следовательно k 1= k 2 - условие параллельности прямых. Если прямые перпендикулярны, то 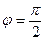 ,
, 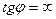 (не существует). Для этого должно выполняться условие
(не существует). Для этого должно выполняться условие 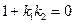 или k 1 k 2=−1, откуда k 1=−1/ k 2 - получено необходимое и достаточное условие перпендикулярности прямых.
или k 1 k 2=−1, откуда k 1=−1/ k 2 - получено необходимое и достаточное условие перпендикулярности прямых.
|
|
|
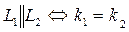 ;
; 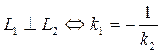
 2014-02-05
2014-02-05 1881
1881
