Дифференциальные уравнения. Основные понятия

Определение 1. Уравнение, связывающее независимые переменные x_i, искомую функцию y и производные различных порядков этой функции, называется дифференциальным уравнением.

Если искомая функция y зависит только от одной переменной, то дифференциальное уравнение называется обыкновенным и записывается в виде

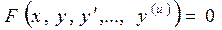, (13.3)

Порядок старшей производной, входящий в уравнение, называется порядком дифференциального уравнения. В частности, уравнение 1-го порядка имеет вид 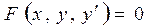(13.4)

Рассмотрим дифференциальные уравнения 1-го порядка.

Простейшим дифференциальным уравнением 1-го порядка является отыскание первообразной функции f(x). Действительно, если 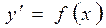, то

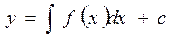(13.5)

В данном случае дифференциальное уравнение имеет бесчисленное множество (семейство) решений. Задача отыскания решения всякого дифференциального уравнения сводится к отысканию всех его решений. Эта задача называется интегрированием дифференциального уравнения.

Из решения (13.5) обнаруживаем, что оно содержит произвольную постоянную C.

Определение. Функция 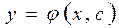называется решением дифференциального уравнения, если при подстановке ее в уравнение вместе о своей производной обращает его в тождество, то есть

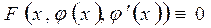
При каждом фиксированном значении постоянной 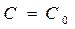, получаем некоторое решение 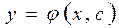, называемое частным решением.

Определение. Совокупность функций 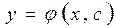, где с - произвольная постоянная, всех частных решений называется общим решением дифференциального уравнения 1-го порядка.

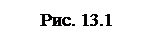
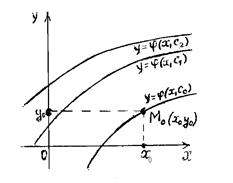Всякое частное решение 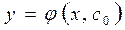геометрически определяет некоторую кривую, называемую нтегральной кривой. Общее решение 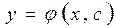, определяет множество (семейство) всех интегральных кривых (рис.13.1).

Если требуется из семейства кривых выделить некоторую определенную кривую, необходимо задать дополнительные условия. Для этого достаточно указать точку плоскости М_о (x₀ , y₀), через которую проходит искомая интегральная кривая. Эти дополнительные условия называют начальными условиями. Обычно, их записывают в виде 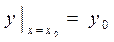. Подставив координаты точки М_о в найденное общее решение, получаем . Отсюда 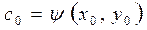, а искомое частное решение имеет вид 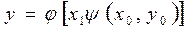. Эта функция определяет искомую интегральную кривую.

Пример. Дано дифференциальное уравнение 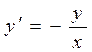. Покажем, что его решением является функция 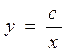. Действительно 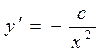подставляем y и y' в заданное уравнение 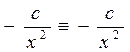. Получено тождество.

Рис.13.2.

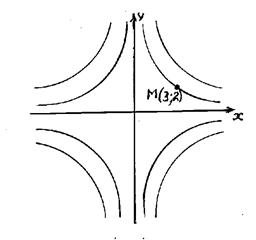
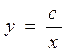Функция определяет множество гипербол (рис.13.2). Выделим ту из них, которая проходит через точку М_о (3, 2). Подставим координаты точки М_о в общее решение 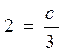, тогда C = 6. Искомое частное решение 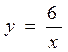- эта функция определяет гиперболу, проходящую через точку М_о (3, 2).

Замечание. Если решение дифференциального уравнения найдено в неявном виде 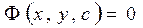его называют общим интегралом.