2014-02-05
493
Если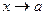 
, но остается меньше а, то говорят о левом пределе функции в точке а и записывают 
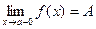; если 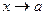,то говорят о правом пределе функции в точке А и записывают 
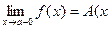> a).
В случае левого предела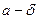 
< x <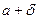
., в случае правого предела 
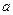< x <.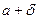
Очевидно, если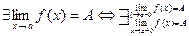 
Есл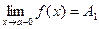и 
и 
, при этом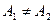 
, то не существует предела 
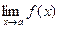(рис.5.2.3).
y
 |
А2
А1
0 а х
Рис.5.2.3
Т.к. определение функции связано с двумя последовательностями: аргументов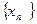 
и значений функции 
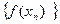, то все теоремы, рассмотренные выше для пределов числовой последовательности, справедливы и для пределов функции.
