1. Оптические свойства вещества в магнитных и электрических полях. Зависимость оптических свойств вещества от магнитного и электрического полей начал изучать ещё Майкл Фарадей в 40-х годах XIX века. Его исследования привели к открытию им магнитооптического эффекта Фарадея - появления оптической активности у веществ, помещенных в магнитное поле и вне поля неактивных. Позднее был открыт электрооптический эффект Керра - появление оптической анизотропии в обычно изотропном веществе, помещенном в электрическое поле (Оптика, §20).
С открытием в 1859 году возможностей спектрального анализа (Г. Кирхгоф, Р. Бунзен) и в связи с быстрым развитием спектроскопии к концу 19 века были созданы спектральные аппараты высокой разрешающей способности. Фиксируя спектры на фотопленку, оказалось возможным не только выявлять очень слабые линии путем увеличения экспозиции, но и очень точно определять положение каждой линии в спектре. Все это позволило перейти от изучения различий между спектрами разных веществ к изучению различий между спектрами одного и того же вещества, испытывающего разные физические воздействия. Из открытых здесь явлений наиболее примечательны эффекты Зеемана и Штарка.
2. Простой эффект Зеемана. В 1896 году, исследуя влияние магнитного поля на излучающее вещество, Питер Зееман обнаружил расщепление спектральных линий под действием магнитного поля. Различают простой эффект Зеемана, когда синглет расщепляется в триплет, и сложный эффект Зеемана, когда дублет расщепляется в мультиплет.
Простой эффект наблюдался на парах кадмия, помещённых в магнитное поле (рис.49). Каждая спектральная линия расщеплялась на несколько компонент в зависимости от того, в каком направлении по отношению к силовым линиям поля ведётся наблюдение.



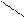 Если свет наблюдается в направлении, перпендикулярном направлению магнитного поля В (поперечный эффект Зеемана), то каждая линия расщепляется на три (синглет ® триплет). Все компоненты триплета линейно поляризованы, (двусторонние стрелки на рисунке показывают направление поляризации), тогда как в отсутствие поля В излучение, дающее линию n 0, не поляризовано. Несмещённую линию называют p - компонентой, плоскость колебаний вектора Е в ней параллельна направлению магнитного поля В. Две симметрично смещённые линии называют s - компонентами, плоскость колебаний вектора Е в них перпендикулярна направлению поля В.
Если свет наблюдается в направлении, перпендикулярном направлению магнитного поля В (поперечный эффект Зеемана), то каждая линия расщепляется на три (синглет ® триплет). Все компоненты триплета линейно поляризованы, (двусторонние стрелки на рисунке показывают направление поляризации), тогда как в отсутствие поля В излучение, дающее линию n 0, не поляризовано. Несмещённую линию называют p - компонентой, плоскость колебаний вектора Е в ней параллельна направлению магнитного поля В. Две симметрично смещённые линии называют s - компонентами, плоскость колебаний вектора Е в них перпендикулярна направлению поля В.
Если наблюдение ведётся вдоль магнитного поля (продольный эффект Зеемана), то в спектре остаются лишь s - компоненты, а p - компонента отсутствует. Обе s - компоненты в продольном эффекте поляризованы по кругу навстречу друг другу. Интенсивность s - компонент в продольном эффекте такая же, как и в поперечном эффекте.
Эффект Зеемана очень слаб. Он наблюдается лишь в сильных магнитных полях с индукцией более 1 Тл. В пределах от 1 до 30 Тл величина расщепления линий D n пропорциональна индукции магнитного поля В. Чем меньше ширина спектральной линии, тем удобнее она для наблюдения. Поэтому основные результаты в опытах Зеемана получены для очень узкой зелёно-голубой линии кадмия (l = 509 нм).
3. Качественное объяснение простого эффекта Зеемана в классической модели Лоренца. Первое объяснение эффекта Зеемана дал Гендрик Лоренц в 1897 году. Лоренц рассматривал оптический электрон в атоме как гармонический осциллятор с частотой n 0, излучающий в отсутствие внешнего магнитного поля спектральную линию этой частоты n 0.
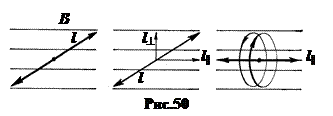 В однородном внешнем магнитном поле В движение линейно колеблющегося электрона (рис.50, слева) можно разложить на две составляющих. Одно колебание совершается вдоль по полю, его амплитуда l ||, другое – поперёк, его амплитуда l ^ (рис.50, в середине). Оба колебания совершаются синхронно с одинаковой частотой n 0. Линейное колебание l ^, совершающееся перпендикулярно полю, можно представить как сумму двух круговых встречных колебаний (рис.50, справа). В результате таких рассуждений линейные колебания электрона в атоме распадаются на сумму трёх колебаний – одного линейного вдоль поля (l ||) и двух встречных круговых в плоскости, перпендикулярной полю.
В однородном внешнем магнитном поле В движение линейно колеблющегося электрона (рис.50, слева) можно разложить на две составляющих. Одно колебание совершается вдоль по полю, его амплитуда l ||, другое – поперёк, его амплитуда l ^ (рис.50, в середине). Оба колебания совершаются синхронно с одинаковой частотой n 0. Линейное колебание l ^, совершающееся перпендикулярно полю, можно представить как сумму двух круговых встречных колебаний (рис.50, справа). В результате таких рассуждений линейные колебания электрона в атоме распадаются на сумму трёх колебаний – одного линейного вдоль поля (l ||) и двух встречных круговых в плоскости, перпендикулярной полю.
Излучение монохроматического света рассматривается Лоренцом как результат колебательного движения электрона. При включении внешнего магнитного поля В на движущийся со скоростью v электрон действует сила Лоренца 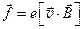 . (8.1)
. (8.1)
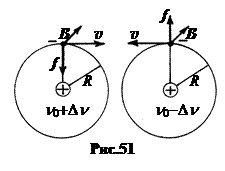 Колебание вдоль по полю не испытывает влияния поля, поэтому оно совершается с неизменённой частотой n 0. Действие же поля на круговые компоненты сводятся к появлению добавочной силы ± evB, направленной вдоль по радиусу круговой траектории к центру (рис.51, слева) или в противоположную сторону (рис.51, справа) в зависимости от знака заряда и направления скорости его движения. Это приводит к изменению частоты вращательного движения на одну и ту же величину ±D n, зависящую от индукции поля В.
Колебание вдоль по полю не испытывает влияния поля, поэтому оно совершается с неизменённой частотой n 0. Действие же поля на круговые компоненты сводятся к появлению добавочной силы ± evB, направленной вдоль по радиусу круговой траектории к центру (рис.51, слева) или в противоположную сторону (рис.51, справа) в зависимости от знака заряда и направления скорости его движения. Это приводит к изменению частоты вращательного движения на одну и ту же величину ±D n, зависящую от индукции поля В.
Итак, движение оптического электрона в атоме при наложении внешнего магнитного поля может быть представлено тремя движениями. Одно линейное колебательное движение по полю с частотой n 0, одно круговое с частотой n 0 + D n в плоскости, нормальной к полю и одно круговое с частотой n 0 - D n в плоскости, нормальной полю. Каждое колебание излучает волну собственной частоты. На рис.52 траектории этих движений одного и того же электрона для удобства восприятия пространственно разнесены.
 В направлении, перпендикулярном магнитному полю В (поперечный эффект), наблюдается p - компонента с частотой n 0 и две линейно поляризованные s - компоненты с частотами n 0 + D n и n 0 - D n. Дело в том, что круговые движения электрона при наблюдении в этом направлении проектируются в линейные.
В направлении, перпендикулярном магнитному полю В (поперечный эффект), наблюдается p - компонента с частотой n 0 и две линейно поляризованные s - компоненты с частотами n 0 + D n и n 0 - D n. Дело в том, что круговые движения электрона при наблюдении в этом направлении проектируются в линейные.
В направлении вдоль магнитного поля (продольный эффект) p - компонента не излучается. Электромагнитная волна излучается лишь в тех направлениях, проекция траектории движения электрона на нормаль к которому не равна нулю (см. Электричество. §22). Круговые колебания электрона создают в этом направлении две циркулярно поляризованные волны с частотами n 0 +D n и n 0 – D n. Направление закручивания компонент зависят от того, какой заряд отрицательный или положительный излучает волну. Если колеблется отрицательный заряд, то “красная” линия n 0 - D n закручена влево, а “фиолетовая” n 0 +D n – вправо.
4. Количественное содержание теории Лоренца сводится к определению величины расщепления D n. С этой целью определяется изменение угловой скорости вращения D w оптического электрона при наложении на излучающий атом внешнего магнитного поля В. В настоящем курсе эта задача решалась при объяснении природы диамагнетизма (см. Электричество, §17). Оказалось, что изменение угловой скорости вращения электрона в атоме (ларморовская частота) определяется формулой: D w = ± eBç 2 mе. (8.2)
Так как D w = 2 p D n, то D n = ± eBç 4 p mе и D l = ± l 2 eBç 4 p mеc. (8.3)
Знак “плюс” у D n соответствует случаю, когда поле В антипараллельно орбитальному магнитному моменту электрона, B ¯ M (на рис.51, слева). Частота обращения электрона в этом случае увеличивается. Знак “минус” соответствует случаю, когда B M (на рис.51, справа). Частота n уменьшается. Величина расщепления D l очень мала. Так, при l = 300 нм в поле 1 Тл D l» 0,004 нм. Это чуть больше 0,001%.
Интересно, что в магнитном поле изменяется скорость обращения оптического электрона на величину D w, но остаётся неизменным радиус вращения. Это строго доказывается в рамках классической электродинамики (см., например, [3], с.с.558-560). Поэтому концепция квантового ротатора со спектром частот, но с постоянным радиусом, упомянутая в §4 на с.21, является вполне корректной.
Формула (8.3) позволяет по данным опыта определить знак и удельный заряд колеблющейся в атоме частицы, излучающей электромагнитную волну. Измерения показали, что этой частицей является электрон.
То, что теория Лоренца, основанная на классических уравнениях Максвелла, столь наглядно и точно! объясняет простой эффект Зеемана, можно объяснить двумя причинами:
Во-первых, оптический электрон кадмия Cd, Z = 48, находится в 5 s – состоянии с нулевым орбитальным моментом. Это можно истолковать так, что электрон движется вдоль по радиусу, что делает его похожим на линейный осциллятор.
Во-вторых, излучающие электроны в многоэлектронных атомах находятся на высоких энергетических уровнях, где величина энергетических ступеней между уровнями становится существенно малой. По принципу соответствия такая система приближается к классической и в некоторых случаях может быть описана в рамках классических моделей.
5. Сложный эффект Зеемана. Дальнейшие исследования показали, что в триплет расщепляются лишь одиночные линии – синглеты. И в целом такой тип расщепления встречается очень редко. Подавляющее число спектральных линий представляют собой мультиплеты, т.е. состоят из нескольких тесно расположенных линий. Простым мультиплетом является дублет натрия – пара линий с длинами волн l 1 = 589,5930 нм и l 2 = 588,9963 нм. Интенсивность линии с меньшей длиной волны l 2 в два раза больше, чем линии l 1. Часто встречаются более сложные мультиплеты, состоящие из многих компонент.
При наложении внешнего магнитного поля линии мультиплетов расщепляются более сложным образом, чем рассмотрено выше. Так, дублет натрия расщепляется на 10 линий: 4 компоненты дает линия l 1 и 6 компонент – линия l 2. Расщепление линий мультиплетов в магнитном поле называют сложным эффектом Зеемана.
Общая причина сложного расщепления мультиплетов в том, что помимо электрического заряда электрон обладает ещё спиновым магнитным моментом. Взаимодействие спинового магнитного момента электрона с магнитным полем атома приводит к появлению тонкой структуры спектральных линий, а взаимодействие его с внешним магнитным полем – к сложному расщеплению.
Квантовая теория позволяет рассчитать характер и величину расщепления. Однако она довольно сложна и громоздка. В качестве примера приведём расщепления дублета натрия (главная серия).
Линия l 1: 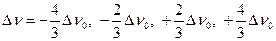 . (8.4)
. (8.4)
Линия l 2: 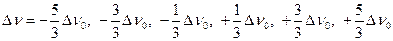 . (8.5)
. (8.5)
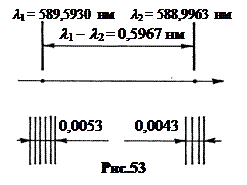 Здесь D n 0 – лоренцово расщепление, определяемое формулой (8.3). В поле с индукцией B = 1 Тл D n 0 = 1,4·1010 с-1, D l 0 = 0,0016 нм. Величина расщепления линии l 1 (расстояние между крайними линиями) составляет 0,0043 нм. У линии l 2 расщепление составляет 0,0053 нм. Для сравнения: расстояние между линиями l 1 и l 2 в дублете натрия равно l 1 - l 2 = 0,5967 нм, т.е. более чем в 300 раз превышает лоренцово расщепление. Величина смещения в сложном эффекте всегда составляет рациональную дробь нормального лоренцова смещения.
Здесь D n 0 – лоренцово расщепление, определяемое формулой (8.3). В поле с индукцией B = 1 Тл D n 0 = 1,4·1010 с-1, D l 0 = 0,0016 нм. Величина расщепления линии l 1 (расстояние между крайними линиями) составляет 0,0043 нм. У линии l 2 расщепление составляет 0,0053 нм. Для сравнения: расстояние между линиями l 1 и l 2 в дублете натрия равно l 1 - l 2 = 0,5967 нм, т.е. более чем в 300 раз превышает лоренцово расщепление. Величина смещения в сложном эффекте всегда составляет рациональную дробь нормального лоренцова смещения.
На рис.53 показана схема расщепления дублета натрия. Расстояние между линиями l 1 и l 2 по сравнению с масштабом расщепления уменьшено на рисунке в 10 раз.
6. Эффект Штарка. Поскольку основным элементом, определяющим оптические свойства атома, является электрон – электрически заряженная частица, то можно предположить, что электрическое поле также должно влиять на частоту испускаемого света.
Но если атом является строго квазиупругим резонатором, совершающим гармонические колебания, то влияние постоянного электрического поля не должно наблюдаться. Постоянная электрическая сила eE, действующая на колеблющийся электрон, должна смещать лишь центр равновесия электрона, не влияя ни на амплитуду, ни на частоту его колебаний. Если колебания резонатора не являются строго гармоническими, то при наложении электрического поля должно наблюдаться слабое расщепление спектральных линий. Экспериментальное изучение этого явления осложняется тем, что трудно создать электрическое поле высокой напряжённости в объёме излучающего газа вследствие сильной его ионизации.
Проблему решил Иоганн Штарк в 1913 г. Он пространственно отделил область высокого напряжения от области ионизации газа. Схема установки Штарка показана на рис.54. Из сосуда, заполненного водородом, из узкого пространства между пластиной F и сеткой с отверстиями К (катод) непрерывно откачивался газ. Благодаря этому здесь было низкое давление и ионизации газа из-за столкновений практически не происходило.
 Пространство между сетчатым катодом К и анодом А, между которыми создавалось поле с напряжением 5000¸10000 В, представляло собой обычную газоразрядную трубку. В направлении слева направо (по рисунку) двигались катодные лучи – электроны, в направлении справа налево – каналовые лучи – положительно заряженные ионы водорода. Проскакивая сквозь отверстие в катоде К, ионы попадали в узкое пространство FK, ширина которого 1 мм. Между электродами F и К создавалось поле 10000 В, напряжённость которого из-за малости расстояния FK достигало большой величины 10000 ç 1·10-3 = 107 В ç м. Присоединяя электроны (рекомбинируя), атомы водорода “высвечивались”. Этот свет наблюдался в направлении, показанном стрелкой (как поперечный эффект Зеемана).
Пространство между сетчатым катодом К и анодом А, между которыми создавалось поле с напряжением 5000¸10000 В, представляло собой обычную газоразрядную трубку. В направлении слева направо (по рисунку) двигались катодные лучи – электроны, в направлении справа налево – каналовые лучи – положительно заряженные ионы водорода. Проскакивая сквозь отверстие в катоде К, ионы попадали в узкое пространство FK, ширина которого 1 мм. Между электродами F и К создавалось поле 10000 В, напряжённость которого из-за малости расстояния FK достигало большой величины 10000 ç 1·10-3 = 107 В ç м. Присоединяя электроны (рекомбинируя), атомы водорода “высвечивались”. Этот свет наблюдался в направлении, показанном стрелкой (как поперечный эффект Зеемана).
Штарк исследовал расщепление спектральных линий водородной серии Бальмера. Расщепление в водороде, а так же в случае всех одноэлектронных ионов оказалось пропорциональным не квадрату напряжённости электрического поля, как это прогнозировалось из теории ангармонического осциллятора, а первой степени напряжённости, т.е. оказалось более сильным. Поэтому такое расщепление называют линейным эффектом Штарка (D n ~ E 0).
Расщепление линий оказалось очень сложным. Так, линия Ha c l = 656,285 нм распалась на 16 компонент, Hb с l = 486,132 нм – на 20 компонент, Hg с l = 434,046 нм распалась на 28 компонент и Hd с l = 410,173 нм – на 32 компоненты. Ширина расщепления, т.е. расстояние между крайними линиями в поле с напряжённостью E = 10,4 МВ ç м составила 2,3 нм для Ha , 3,88 нм для Hb , 5.88 нм для Hg , 7,5 нм для Hd . Если сравнивать с расщеплением Зеемана в магнитном поле B» 10,4 Тл, то расщепление Штарка больше чем на порядок.
При наблюдении поперёк поля все p - компоненты линейно поляризованы параллельно Е 0 внешнего поля, а s - компоненты поляризованы перпендикулярно Е 0. При наблюдении вдоль поля p - компоненты не появляются, а s - компоненты не поляризованы.
Многоэлектронные атомы дают квадратичный эффект, D n ~ 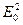 . Именно такой эффект прогнозировался в теории ангармонического осциллятора. Квадратичный эффект существенно слабее линейного.
. Именно такой эффект прогнозировался в теории ангармонического осциллятора. Квадратичный эффект существенно слабее линейного.
С момента открытия эффекта Штарка стало ясно, что законы классической электродинамики не могут объяснить это явление. Последовательную теорию эффекта удалось построить только в рамках квантовой механики. Эта теория сложна и громоздка, и потому в учебных курсах не излагается (см., например, [2, 4]).
Заметим лишь, что линейный эффект Штарка реализуется у атомов, имеющих дипольный электрический момент в отсутствие внешнего электрического поля E 0. Если у атома нет собственного электрического момента, то реализуется квадратичный эффект Штарка. Расщепление возникает благодаря тому, что электрический момент у атома индуцируется внешним электрическим полем E 0.
7. Количественные критерии сильного и слабого полей. Магнитное поле считается слабым, если лоренцово расщепление D n 0много меньше расщепления D n, обусловленного спин-орбитальным взаимодействием. 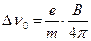 <<D n. Поле В слабое. (8.6)
<<D n. Поле В слабое. (8.6)
Обычно поле считается слабым, когда 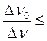 10-3 (В < 1 Тл).
10-3 (В < 1 Тл).
Электрическое поле считается слабым, когда штарковское расщепление D n 0меньше мультиплетного, D n 0 < D n. Если D n 0 > D n, электрическое поле считается сильным (E ³ 105 В ç м).
 2014-02-02
2014-02-02 5901
5901








